(a) A rod of length l is moved horizontal with a uniform velocity v in a direction perendicular to its length through a region in which a uniform magnetic field is acting vertically downward. Derive the expression for the emf induced across the end of the rod.
(b) How does one understand this motional emf by invoking the Lorentz force acting on the free charge carriers of the conductor? Explain.
The conductor is moving in a direction perpendicular to the field with constant velocity under the influence of some external agent.
The electrons in the conductor experience a force
→F=q(→v×→B)
That is directed along the length l perpendicular to both v to B
Under the influence of this force, the electrons move to the lower end of the conduction and accumulate there leaving a net positive charge at the upper end.As a result of this charge separation an electric field is product inside the conductor.The charges accumulate at both ends until the downward magnetic force qvB is balanced by the upward electric force qE.At this point, electrons stop moving .The condition of equilibrium requires that
q[→E+(→v×→B)]=0
→E=−(→v×→B)
V=−∫→E.d→l
ΔV=(→v×→B).→l
=V⊥l⊥v
B⊥ is the component of magnetic field perpendicular to the velocity.
(a)ϕB=Blx
ε=−dϕBdt=−ddt(Blx)
ε=Blv



Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-3 PART 2
16 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
A conducting rod of unit length moves with a velocity of 5m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.4T. Find the emf induced between the ends of the stick.
View SolutionA metallic rod of length l is moved perpendicular to its length with velocity v in a magnetic field →B acting perpendicular to the plane in which rod moves. Derive the expression for the inducced emf.
View Solution
Knowledge Check
A rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
ABl2ω2BzeroC(Bl2ω8)D2Bl2ω
A small conducting rod of length l, moves with a uniform velocity v in a uniform magnetic field B as shown in fig __

View SolutionA metallic wire PQ of length 1cm moves with a velocity of 2m/s in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2T.Find the emf induced between the ends of the wire.Which end will be positively charged.

View SolutionA conductor of length 0.1m is moving with a velocity of 4m/ s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
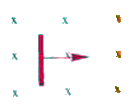
View SolutionA conductor of length 0.1m is moving with a velocity of 4m/s in a uniform magnetic field of 2T as shown in the figure. Find the emf induced ?
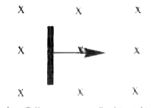
View SolutionA metal rod moves at a constant velocity in a direction perpendicular to its length. A constant, uniform magnetic field exists in space in a direction perpendicular to the rod as well as its velocity. Select the correct statements(s) from the following
View SolutionA rod of length l rotates with a uniform angular velocity omega about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the lrod is
View SolutionA semicircular conducting wire of radius a is moving perpendicular to a uniform magnetic field B with speed√2vas shown in the figure.The emf induced across the wire Is
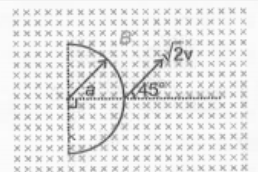
View Solution
