Question

An equil convex lens of focal length ${\displaystyle 10cm}$ (in air) and ${\displaystyle R.l.4/3}$ is put at a small opening on a tube of length ${\displaystyle 1m}$ fully filled with liquid of ${\displaystyle R.l.4/3.A}$ concave mirror of radius of curvature ${\displaystyle 20cm}$ is cut into two halves ${\displaystyle m_1\text{and}{m}_2}$ and placed at the end of the tube. ${\displaystyle m_1\&m_2}$ are placed such that thir principal axis ${\displaystyle AD,\text{and}CD}$ respectively are separated by ${\displaystyle 1mm}$ each from the principal axis of the lens. ${\displaystyle A}$ slit ${\displaystyle S}$ placed in air illuminates the lens with light of frequency ${\displaystyle 7.5\times {10}^{14}Hz.}$ The light reflected from ${\displaystyle m_1\text{and}{m}_2}$ forms interference pattern on the left end ${\displaystyle EF}$ of the tube. ${\displaystyle O}$ is an opaque substance to cover the hole left by ${\displaystyle m_1\&m_2.}$ Find :

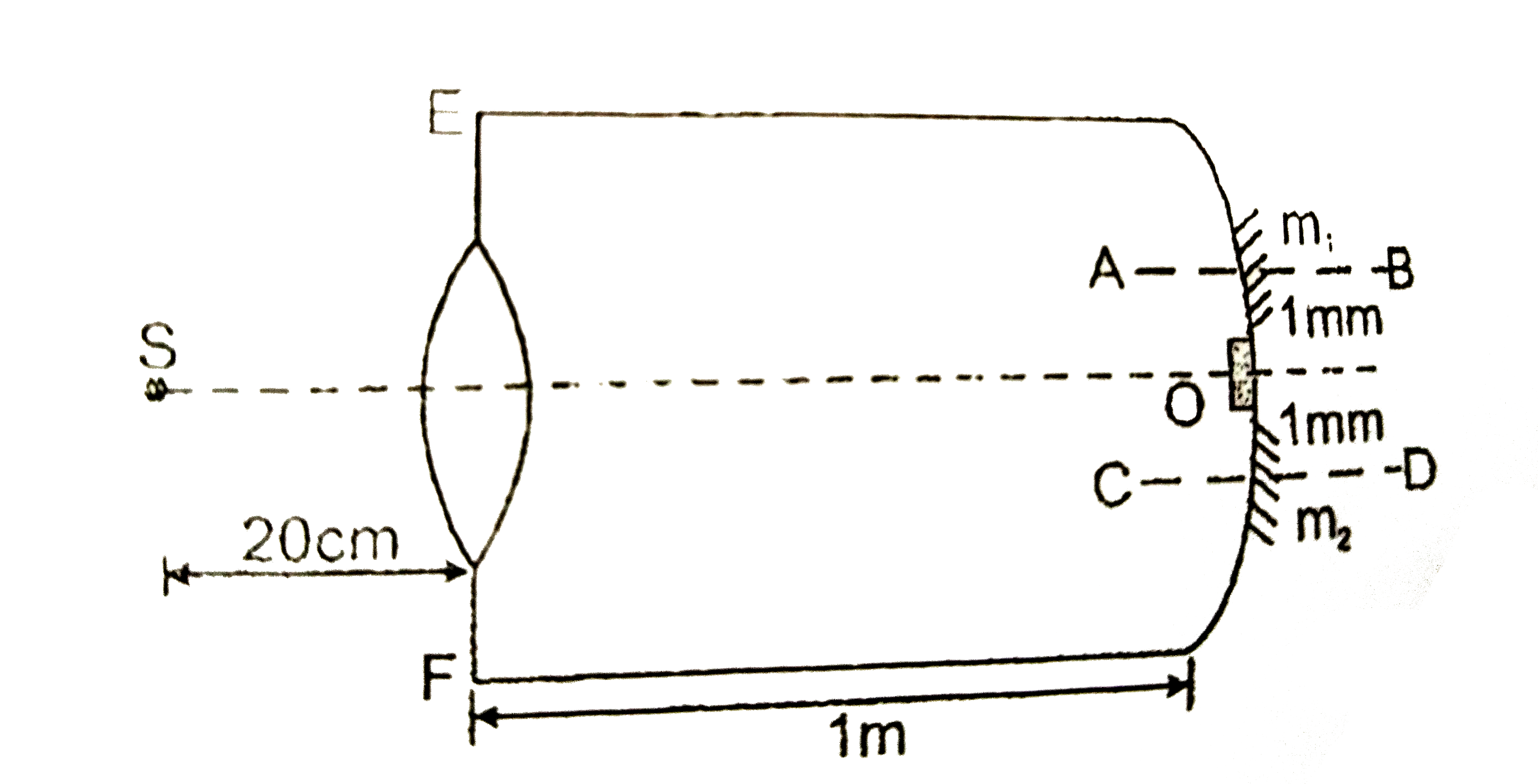
(a) the position of the iamge formed by lens water combination.
(b) the distance between the images formed by ${\displaystyle m_1\&m_2}$.
(c) width of the fringes on ${\displaystyle EF}$

Answer

(a) `80 cm` behind the lens
(b) `4 mm`
(c) `beta =60 mum`

Explanation

Lets find out the radius of curvature of equi. Convex lens.
`(1)/(f)=(mu-1)((1)/(R)-(1)/(-R)) rArr (1)/(10)=((3)/(2)-1)((2)/(R)) rArr R=10 cm`.
Now

for lins :
`(1)/(V)-(1)/(-20)=(1)/(10) rArr (1)/(V)=(1)/(20)`
`rArr` for surface of tube (of `R=10 cm`.)
`(mu_(2))/(V)-(mu_(1))/(u)=(mu_(2)-mu_(1))/(R) rArr (4//3)/(V)-(1)/(+20)=(4//3-1)/(-10) rArr V=+80 cm`.
(b) Now for mirrors.

As the object for the mirrors is at `20 cm` so the image will be at `20 cm` only
`therefore u=-2f` also.
`rArr` magnifiction `=m=(y_(1))/(y_(0))=(-v)/(u)`
`rArr (y_(1))/(-(1mm))=^(-)((-20)/(-20)) rArr y_(1)=+(1 mm)`
so the final images are like.

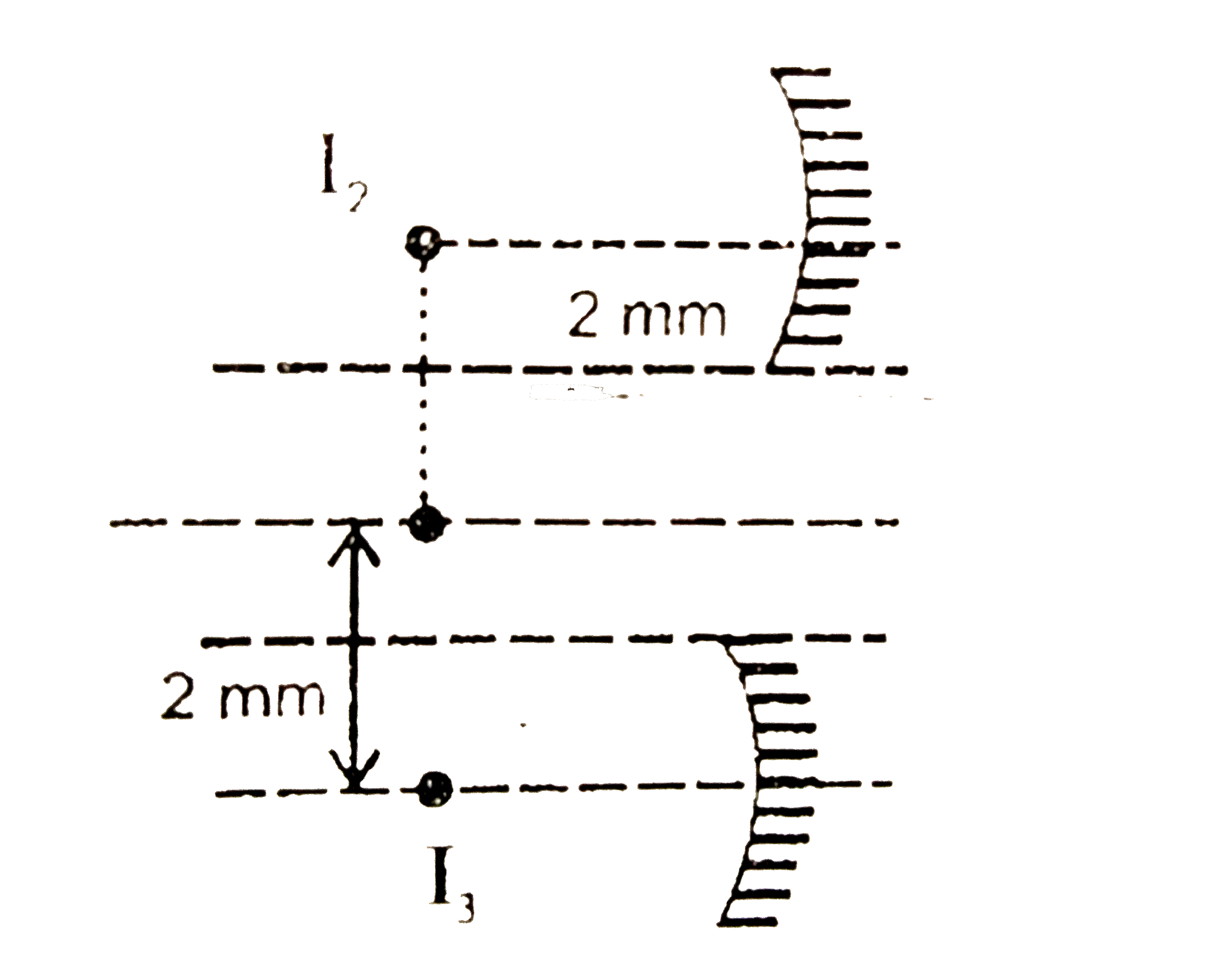
so the distance between the images is `4 mm`.
(c) Now, these `I_(2) and I_(4)` behave as the `2` sources for fringe pattern.
`rArr beta=(lambdaD)/(d)=(vD)/(fd) =((c//mu)D)/(fd)`
`=((3xx10^(8))/((4)/(3)))xx(0.8)/((3)/(3)xx10^(15)xx(4xx10^(3))) =60 mum`.