Derive an expression for the velocity of pulse in a in stretched in string under a tension T and μ is the mass per unit length of the sting.
The correct Answer is:The broad view of the pulse under the tension T is given by
(##RESWFPMPHYXIC05E01014_A01##)
As; 2Tsin(θ)2=dmv2R
⇒2Tθ2=(ml).Rθ(v2))R
⇒v=√Tμ
where μ=ml, is the mass per unit length of the string also known as the linear mass density.
Step by step video & image solution for Derive an expression for the velocity of pulse in a in stretched in string under a tension T and mu is the mass per unit length of the sting. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 1 PART I
23 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 1 PART II
30 Videos
- TRAVELLING WAVESBOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Solved Miscellaneous Problems
7 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
- WAVE ON STRING BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 3 PART II
7 Videos
Similar Questions
The frequency (f) of a stretched string depends upen the tension F (dimensions of form ) of the string and the mass per unit length mu of string .Derive the formula for frequency
View SolutionThe velocity of transverse wave in a string is v=√T/m where T is the tension in the string and m is the mass per unit length . If T=3.0kgf, the mass of string is 25g and length of the string isv=1.000m, then the percentage error in the measurement of velocity is
View SolutionThe frequency v of the stretched string may depend on (i) the length of the vibrating segment 1 (ii) the tension in the string and (iii) the mass per unit length m. Show that v∝1l√Fm.
View SolutionCheck the accuracy of the relation v=12l√Tm,where v is the frequency, l is legth, T is tension and m is mass per unit legth of the string.
View SolutionDerive the expression for the self inductance of a long solenoid of cross sectional area A and length l, having n turns per unit length.
View SolutionFour pieces of string of length L are joined end to end to make a long string of length 4L. The linear mass density of the strings are μ,4μ,9μand16μ, respectively. One end of the combined string is tied to a fixed support and a transverse wave has been generated at the other end having frequency f (ignore any reflection and absorption). string has been stretched under a tension F.

Find the ratio of wavelength of the wave on four string, starting from right hand side.
View SolutionIn each of the four situations of column-I , a stretched string or an organ pipe is given along with the required data. In case of strings the tension in string is T=102.4 N and the mass per unit length of string is 1g/m. Speed of sound in air is 320 m/s. Neglect end corrections.The frequencies of resonance are given in column-II.Match each situation in column-I with the possible resonance frequencies given in Column-II.
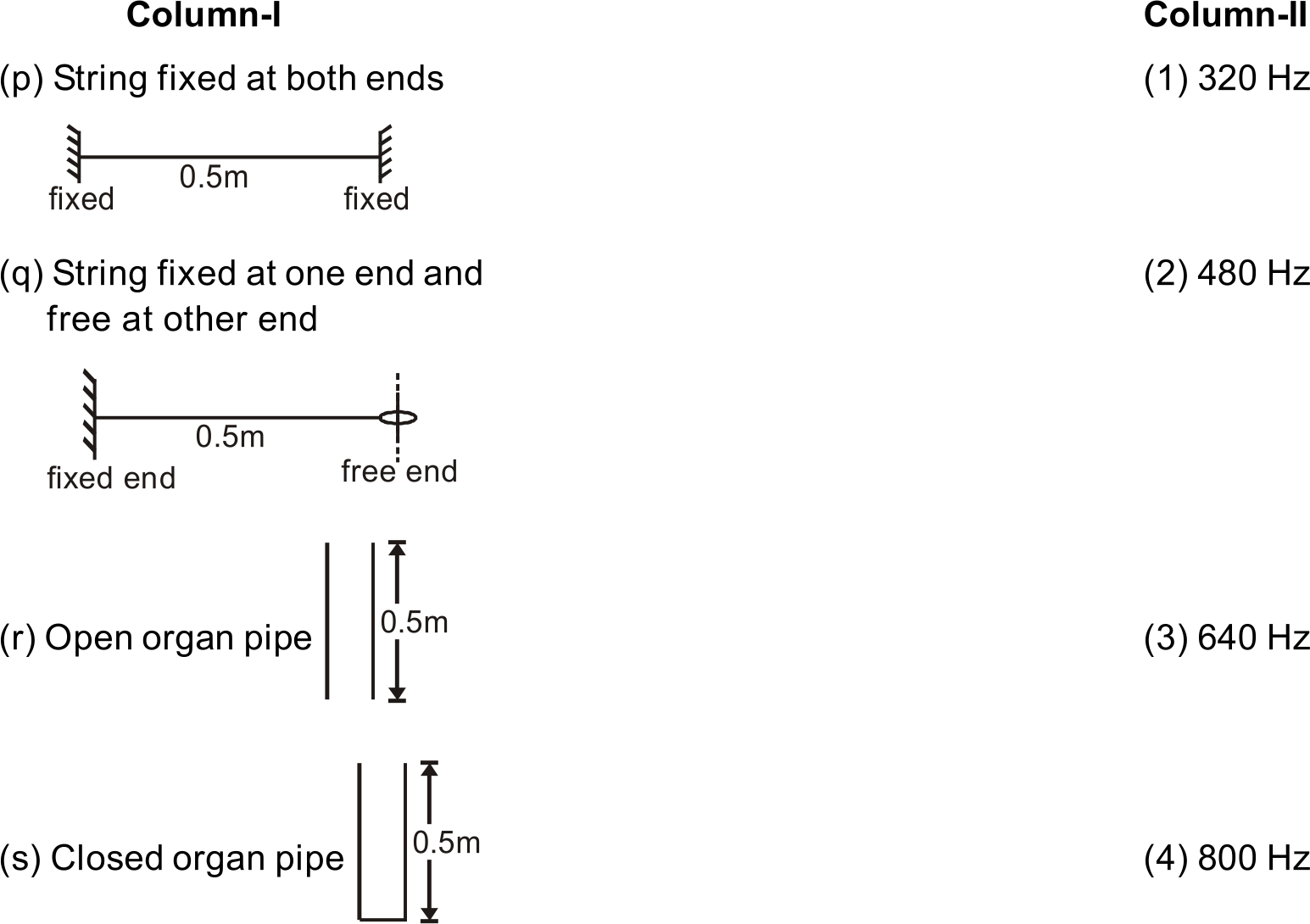
View SolutionThree strings of equal lengths but stretched with different tensions are inade to vibrate. If their masses per unit length are in the ratio 1:2:3 and the frequencies are the same, calculate the ratio of the tensions.
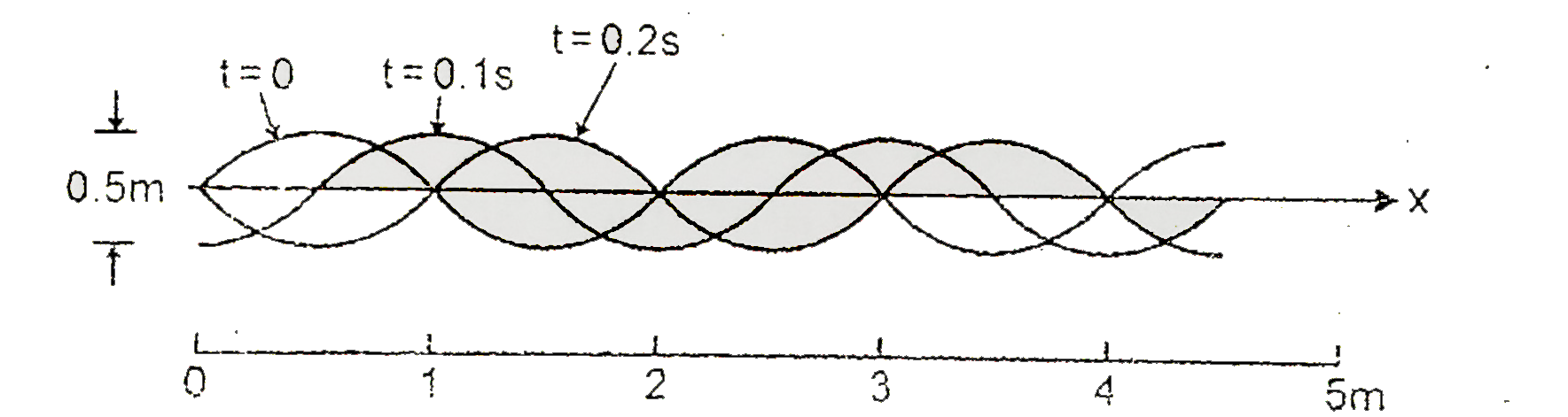
View SolutionThree consecutive flash photographs of a travelling wave on a string wave on a string are reproduced in the figure here. The following oberservation are made. Mark the one which is correct. (Mass per unit length of the sting =3g/cm.)
View SolutionAssertion : Two strins shown in figure have the same tension. Speed of transverse waves in string−1 will be more.
 Reason : v∝1√μ,Heremu is mass per unit length of string.
Reason : v∝1√μ,Heremu is mass per unit length of string.
View Solution
