Question

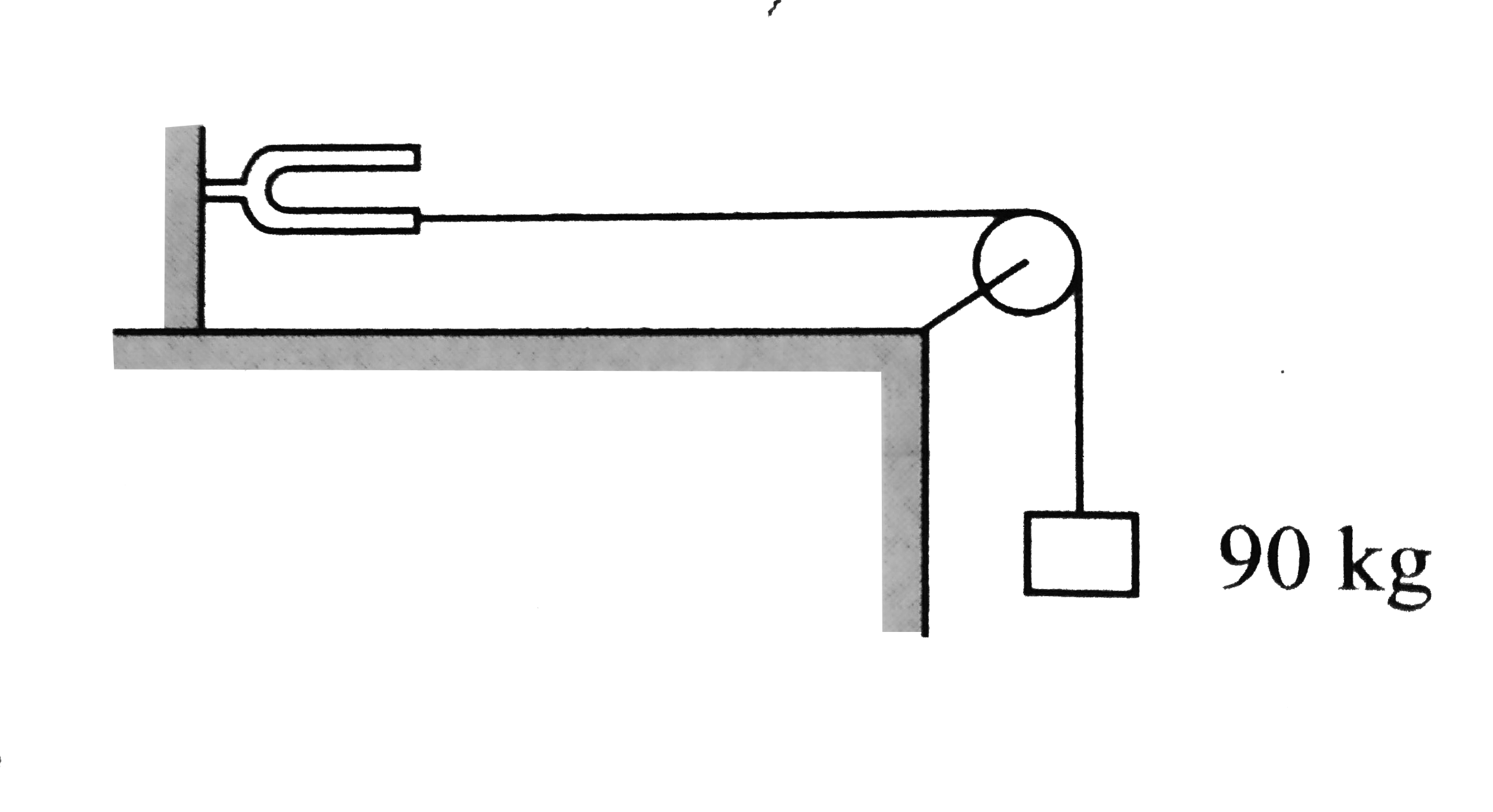
One end of a long string of linear mass dnesity $8.0\times {10}^{-3}kg{m}^{-1}$ is connected to an electrically driven tuning fork of frequency 256 Hz. The other end passes over a pulley and is tied to a pan containing a mass of 90 kg. The pulley end absorbs all the incoming energy so that reflected waves at this end have negligible amplitude. At $t=0$ the left end (fork end) of the string $x=0$ has zero transverse displacement $(y=0)$ and is moving along positive y-direction. The amplitude of the wave is 5.0 cm. Write down the transverse displacement y as function of x and t that describest the wave on the string.

Answer

`y = 0.005 sin (omegat +-kx);` here `omega`
`= 1.61 xx 10^(3) s^(-1) , k = 4.84 m^(-1)`
`x` and `y` are in `m`.

Explanation

To find the transverse displacement $$y$$ as a function of $$x$$ and $$t$$ for the wave on the string, we will follow these steps:

Step 1: Identify the Given Values
- Linear mass density \( \mu = 8.0 \times 10^{-3} \, \text{kg/m} \)
- Frequency \( f = 256 \, \text{Hz} \)
- Mass hanging from the string \( m = 90 \, \text{kg} \)
- Amplitude \( A = 5.0 \, \text{cm} = 0.05 \, \text{m} \)

Step 2: Calculate the Tension in the String
The tension \( T \) in the string due to the hanging mass is given by:
\( T = mg = 90 \, \text{kg} \times 9.8 \, \text{m/s}^2 = 882 \, \text{N} \)

Step 3: Calculate the Velocity of the Wave
The velocity \( v \) of the transverse wave on the string can be calculated using the formula:
\( v = \sqrt{\frac{T}{\mu}} = \sqrt{\frac{882 \, \text{N}}{8.0 \times 10^{-3} \, \text{kg/m}}} \)
Calculating this gives:
\( v \approx \sqrt{110250} \approx 332 \, \text{m/s} \)

Step 4: Calculate the Angular Frequency \( \omega \)
The angular frequency \( \omega \) is given by:
\( \omega = 2\pi f = 2 \times 3.14 \times 256 \approx 1600 \, \text{rad/s} \)

Step 5: Calculate the Wavelength \( \lambda \)
The wavelength \( \lambda \) can be calculated using:
\( \lambda = \frac{v}{f} = \frac{332 \, \text{m/s}}{256 \, \text{Hz}} \approx 1.297 \, \text{m} \)

Step 6: Calculate the Wave Number \( k \)
The wave number \( k \) is given by:
\( k = \frac{2\pi}{\lambda} = \frac{2 \times 3.14}{1.297} \approx 4.84 \, \text{m}^{-1} \)

Step 7: Write the Equation for Transverse Displacement \( y \)
The general form of the wave equation traveling in the positive y-direction is:
\( y(x, t) = A \sin(\omega t - kx) \)
Substituting the values we have:
\( y(x, t) = 0.05 \sin(1600 t - 4.84 x) \)

Final Answer
Thus, the transverse displacement \( y \) as a function of \( x \) and \( t \) is:
\( y(x, t) = 0.05 \sin(1600 t - 4.84 x) \)