Following are equations of four waves :
(i) y1=asinω(t−xv)
(ii) y2=acosω(t+xv)
(iii) z1=asinω(t−xv)
(iv) z1=acosω(t+xv)
Which of the following statements are correct ?
On superposition of wave (i) and (iii), a travelling wave having amplitude a√2 will be formed
Superposition of waves (ii) and (iii) is not possible
On superposition of (i) and (ii), a stationary wave having amplitude a√2 will be formed
On superposition of (iii), and (iv), a transervers stationary wave will be formed
The correct Answer is:A, D
To analyze the given wave equations and determine the correctness of the statements, we will break down the problem step by step.
Step 1: Identify the wave equations
The equations of the waves are:
1. y1=asin(ωt−xv)
2. y2=acos(ωt+xv)
3. z1=asin(ωt−xv)
4. z2=acos(ωt+xv)
Step 2: Determine the direction of wave propagation
- For y1 and z1 (both have the form sin(ωt−xv)):
- The negative sign indicates that these waves are traveling in the positive x-direction.
- For y2 and z2 (both have the form cos(ωt+xv)):
- The positive sign indicates that these waves are traveling in the negative x-direction.
Step 3: Analyze the statements
1. Statement A: "Waves 1 and 3 will form a traveling wave having amplitude a√2."
- Analysis:
- Both y1 and z1 are traveling in the same direction (positive x-direction).
- When two waves of the same amplitude a travel in the same direction, the resultant amplitude is √a2+a2=a√2.
- Conclusion: This statement is correct.
2. Statement B: "Superposition of waves 2 and 3 is not possible."
- Analysis:
- y2 (cosine wave) and z1 (sine wave) can superpose since they are independent of each other and can exist in the same space.
- Conclusion: This statement is incorrect.
3. Statement C: "Superposition of waves 1 and 2 represents a stationary wave having amplitude a√2."
- Analysis:
- y1 travels in the positive x-direction and y2 travels in the negative x-direction.
- The superposition of two waves traveling in opposite directions can form a stationary wave, but the amplitude will not be a√2 since they are not at 90 degrees to each other.
- Conclusion: This statement is incorrect.
4. Statement D: "Superposition of waves 3 and 4 will form a transverse stationary wave."
- Analysis:
- z1 and z2 are traveling in opposite directions (one in positive x-direction and the other in negative x-direction).
- Their superposition will indeed form a stationary wave.
- Conclusion: This statement is correct.
Final Conclusion
- The correct statements are A and D.
The equations of the waves are:
1. y1=asin(ωt−xv)
2. y2=acos(ωt+xv)
3. z1=asin(ωt−xv)
4. z2=acos(ωt+xv)
- For y1 and z1 (both have the form sin(ωt−xv)):
- The negative sign indicates that these waves are traveling in the positive x-direction.
- For y2 and z2 (both have the form cos(ωt+xv)):
- The positive sign indicates that these waves are traveling in the negative x-direction.
1. Statement A: "Waves 1 and 3 will form a traveling wave having amplitude a√2."
- Analysis:
- Both y1 and z1 are traveling in the same direction (positive x-direction).
- When two waves of the same amplitude a travel in the same direction, the resultant amplitude is √a2+a2=a√2.
- Conclusion: This statement is correct.
- Analysis:
- y2 (cosine wave) and z1 (sine wave) can superpose since they are independent of each other and can exist in the same space.
- Conclusion: This statement is incorrect.
- Analysis:
- y1 travels in the positive x-direction and y2 travels in the negative x-direction.
- The superposition of two waves traveling in opposite directions can form a stationary wave, but the amplitude will not be a√2 since they are not at 90 degrees to each other.
- Conclusion: This statement is incorrect.
- Analysis:
- z1 and z2 are traveling in opposite directions (one in positive x-direction and the other in negative x-direction).
- Their superposition will indeed form a stationary wave.
- Conclusion: This statement is correct.
- The correct statements are A and D.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 2 PART IV9videos
TRAVELLING WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 3 PART II7videos
TRAVELLING WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Exercise- 2 PART II19videos
TRAVELLING WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS130videos
TEST SERIES
- BOOK - RESONANCE ENGLISHCHAPTER - WAVE ON STRING EXERCISE - Exercise- 3 PART II7videos
WAVE ON STRING
Similar Questions
If i1=3sinωtand(i2)=4cosωt, then (i3) is
 View Solution
View SolutionFour sound sources produce the following four waves
(i) y1=asin(ωt+ϕ1)
(ii) y2=asin2ωt
(iii) y3=a'sin(ωt+ϕ2)
(iv) y4=a'sin(3ωt+ϕ)
Superposition of which two waves gives rise to interference?View SolutionThe following equations represent progressive transverse waves
z1=Acos(ωt−kx)
z2=Acos(ωt+kx)
z3=Acos(ωt+ky)
z4=Acos(2ωt−2ky)
A stationary wave will be formed by superposingView SolutionIn y= A sin ωt + A sin (ωt+(2π)/3) match the following table.
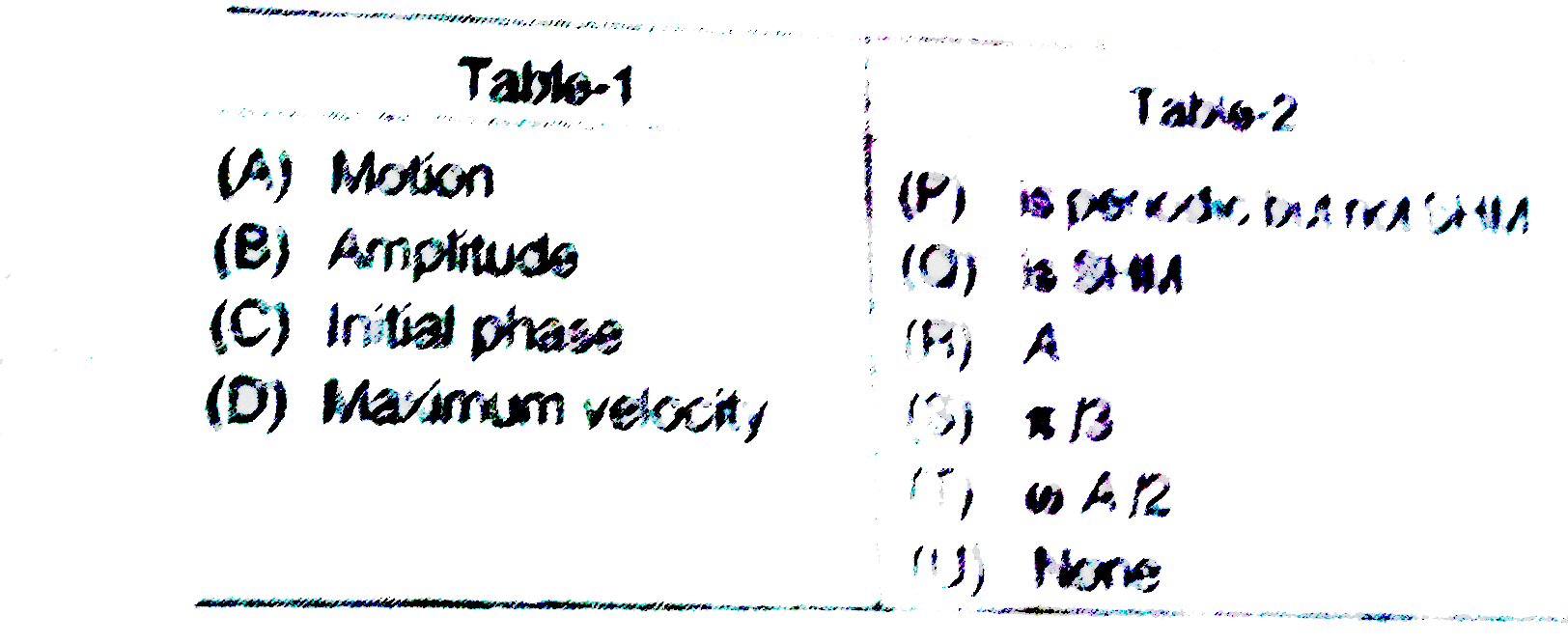 View Solution
View SolutionConsider the three waves z1,z2andz3 as
z1=Asin(kx−ωt)
z2=Asin(kx+ωt)
z3=Asin(ky−ωt)
Which of the following represents a standing wave?View Solutionx1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.View Solutionx1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.View SolutionThe path difference between the two waves
y1=a1sin(ωt−2πxλ)andy(2)=a2cos(ωt−2πxλ+ϕ) isView SolutionThe path difference between the two waves
y1=a1sin(ωt−2πxλ)andy(2)=a2cos(ωt−2πxλ+ϕ) isView Solutionx1=3sinωt,x2=4cosωt
Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.View Solution

