x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
Find amplitude of resultant SHM.
x1=5sinωt
x2=5sin(ωt+53∘)
x3=−10cosωt
we can write x3=10sin(ωt+270∘)
Finding the resultant amplitude by vactor notation.
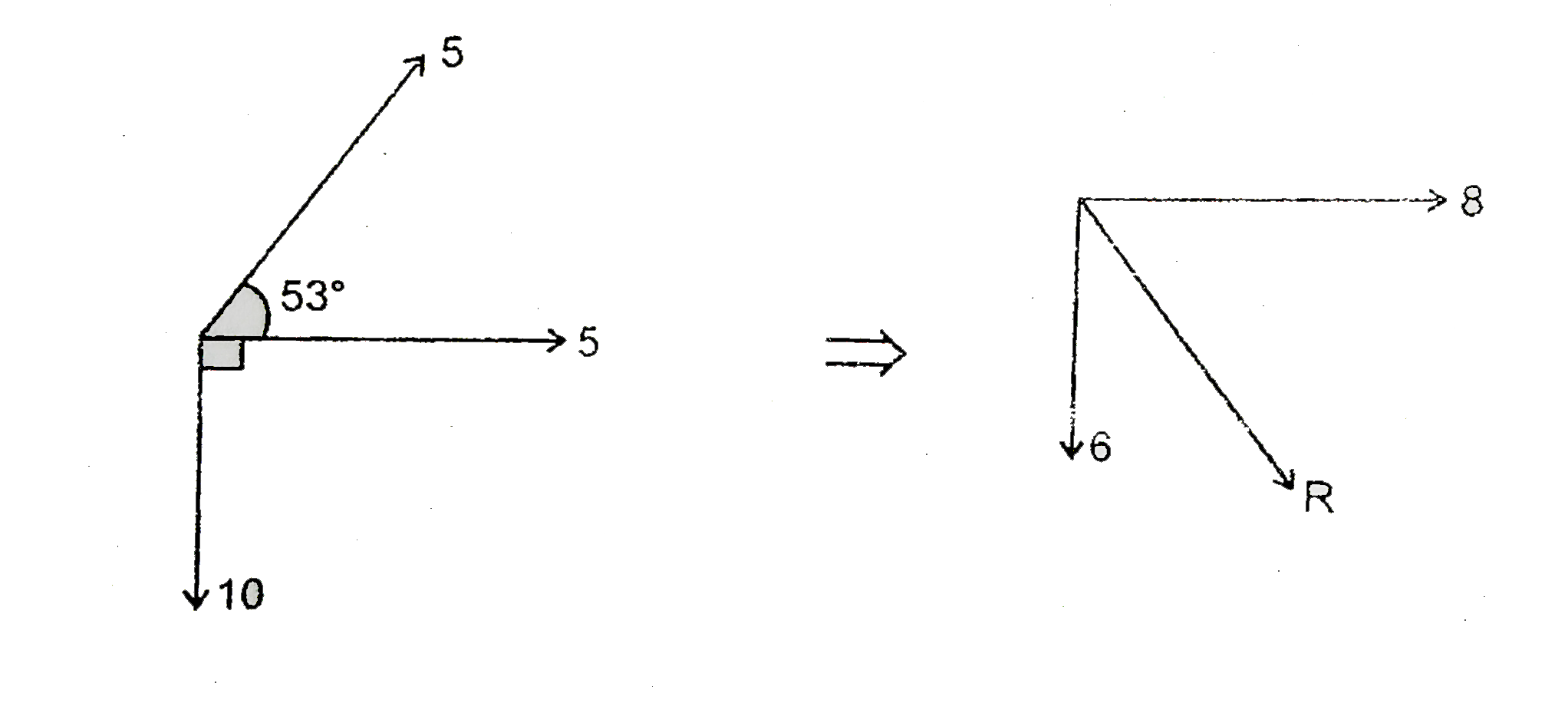
Resultant Amplitude |R|=√82+62=10 Ans.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Board Level Exercise24videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I25videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems13videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCE ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PHYSICS784videos
TEST PAPERS
Similar Questions
x1=5sin(ωt+30∘)
x2=10cos(ωt)
Find amplitude of resultant SHM.View Solutionx1=3sinωt , x2=4cosωt. Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.
View Solutionx1=3sinωt,x2=4cosωt
Find (i) amplitude of resultant SHM, (ii) equation of the resultant SHM.View SolutionTwo simple harmonic motion are represrnted by the following equation y1=40sinωt and y2=10(sinωt+ccosωt). If their displacement amplitudes are equal, then the value of c (in appropriate units) is
View SolutionTwo simple harmonic motion are represrnted by the following equation y1=40sinωt and y2=10(sinωt+ccosωt). If their displacement amplitudes are equal, then the value of c (in appropriate units) is
View Solutionx1=3sinωt⇒x2=4cosωt. Find (i) amplitude of resultant SHm, (ii) equation of the resultant SHm.
View SolutionIf i1=3sinωtand(i2)=4cosωt, then (i3) is
 View Solution
View SolutionThe resultant amplitude due to superposition of three simple harmonic motions x1=3sinωt,
x2=5sin(ωt+37∘) and x3=−15cosωt isView SolutionA particle is subjected to SHM as given by equations x1=A1sinωt and x2=A2sin(ωt+π/3).The maximum acceleration and amplitude of the resultant motion are it amax and A,respectively , then
View SolutionTwo SHM's are represented by y1=Asin(ωt+ϕ),y2=A2[sinωt+√3cosωt]. Find ratio of their amplitudes.
View Solution
