Rotational energy levels of diatomic molecules are well described by the formula $E_{J} = B J (J + 1)$ , where $J$ is the rotational quantum number of the molecule and $B$ its rotational constant. $B$ is related to the reduced
mass $μ$ and the bond length $R$ of the molecule through the equation $B = \frac{h^{2}}{8 π^{2} μ R^{2}}$ .
In general, spectroscopic transitions appear at photon energies which are equal to the energy difference between appropriate states of a molecule $(h v = Δ E)$ . The observed rotational transitions occur between adjacent rotational levels, hence $Δ E = E_{J + 1} - E_{J} = 2 B (J + 1)$ . Consequently, successive rotational transitions that appear on the spectrum (such as the one shown here) follow the equation $h (Δ υ) = 2 B$ .

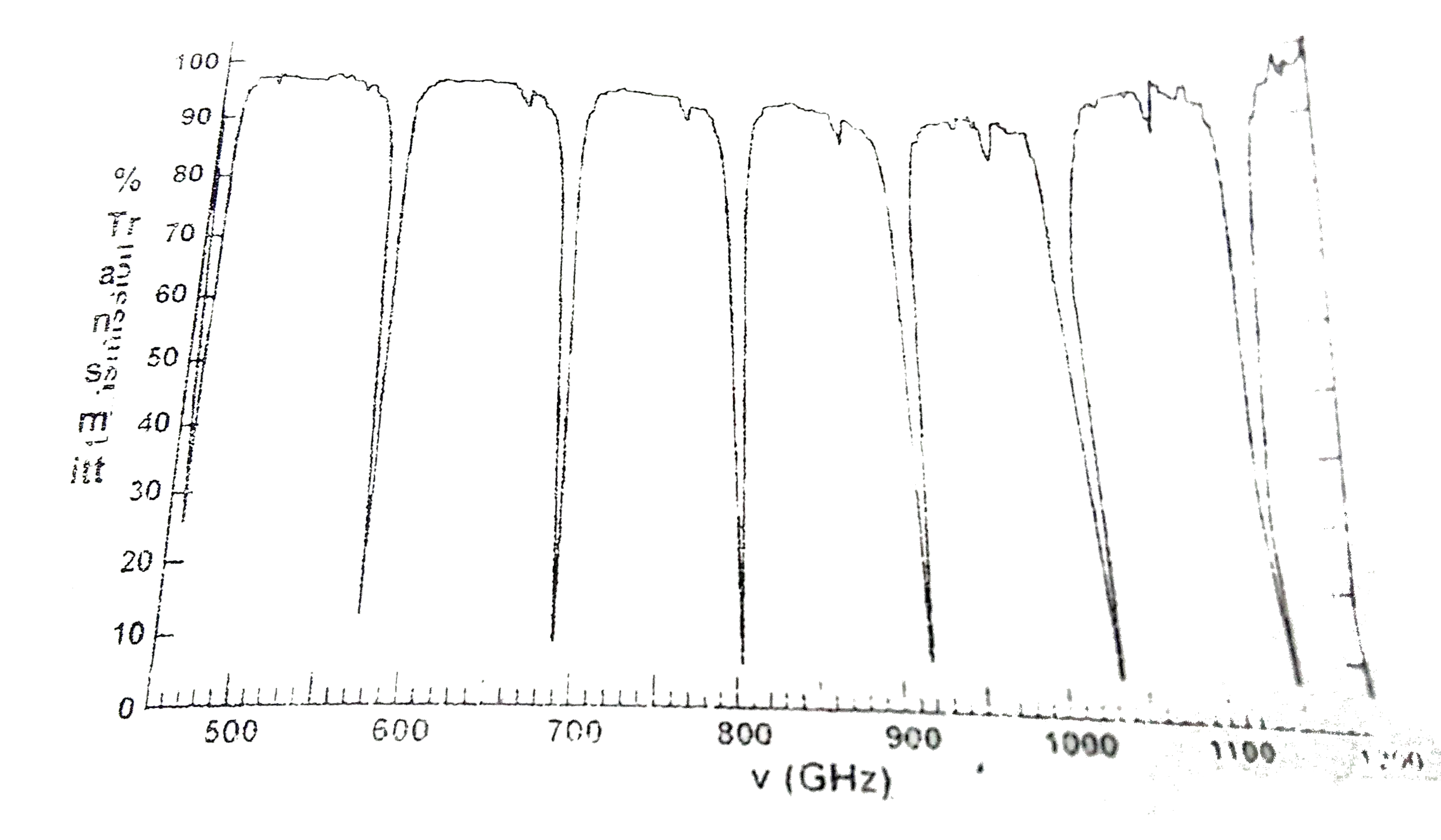
By inspecting the spectrum provided, determine the following quantities for $^(2) C^{p} C$ with appropriate units
(a) $Δ υ$ (b) $B$ (c) $R$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:{:a) For example : $Δ V = 1150 - 1035 = 115 G H z$
{:b) $B = \frac{h Δ v}{2} = \frac{6.63 \times 10^{- 34} \times 115' \times 10^{9}}{2} = 3.81 \times 10^{- 23} J$
{:c) $μ = \frac{m (C) \times m (O)}{m (C O)} = \frac{12 \times 16}{28} = 6.86 a . u . = 1, 14 \times 10^{- 26} k g$
For interatomic distance R:
$R = \frac{h}{2 π \sqrt{2 μ B}} = \frac{3.63 \times 10^{- 34}}{2 \times 3.14 \sqrt{2 \times 1.14 \times 10^{- 26} \times 3.81 \times 10^{- 23}}} = 1.13 \times 10^{- 10} m = 1.13 Å$

Answer

Step by step video & image solution for Rotational energy levels of diatomic molecules are well described by the formula E_(J)=BJ(J+1), where J is the rotational quantum number of the molecule and B its rotational constant. B is related to the reduced mass mu and the bond length R of the molecule through the equation B=h^(2)/(8pi^(2)muR^(2)). In general, spectroscopic transitions appear at photon energies which are equal to the energy difference between appropriate states of a molecule (hv=DeltaE). The observed rotational transitions occur between adjacent rotational levels, hence DeltaE=E_(J+1)-E_(J)=2B(J+1). Consequently, successive rotational transitions that appear on the spectrum (such as the one shown here) follow the equation h(Deltaupsilon)=2B. By inspecting the spectrum provided, determine the following quantities for ^(2) C ^(p)C with appropriate units (a) Deltaupsilon (b) B (c) R by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 CHEMISTRY CHEMICAL KINETICS

Similar Questions

Recommended Questions

The correct Answer is:{:a) For example : ΔV=1150−1035=115GHz {:b) B=hΔv2=6.63×10−34×115'×1092=3.81×10−23J {:c) μ=m(C)×m(O)m(CO)=12×1628=6.86a.u.=1,14×10−26kg For interatomic distance R: R=h2π√2μB=3.63×10−342×3.14√2×1.14×10−26×3.81×10−23=1.13×10−10m=1.13Å

Similar Questions

Recommended Questions