A insulated piston freely move in a cyclinder from volume 5 lit to 10 lit then calculate work done & heat during this expansion.
To solve the problem of calculating the work done and heat during the expansion of an insulated piston moving from a volume of 5 liters to 10 liters, we can follow these steps:
Step 1: Understand the System
We have an insulated piston, which means that there is no heat exchange with the surroundings. The piston moves from an initial volume (V1) of 5 liters to a final volume (V2) of 10 liters.
Step 2: Calculate Work Done
The work done (W) during an expansion can be calculated using the formula:
W=−Pexternal×(V2−V1)
Where:
- Pexternal is the external pressure acting on the piston.
- V1 is the initial volume.
- V2 is the final volume.
Since the piston is insulated and moves freely, there is no external pressure acting on it:
Pexternal=0
Thus, substituting this into the work done formula:
W=−0×(10lit−5lit)=0
Step 3: Apply the First Law of Thermodynamics
According to the first law of thermodynamics:
ΔU=Q+W
Where:
- ΔU is the change in internal energy.
- Q is the heat added to the system.
- W is the work done on the system.
From step 2, we found that W=0. Therefore, the equation simplifies to:
ΔU=Q+0⇒ΔU=Q
Step 4: Determine Change in Internal Energy
In an insulated system, where there is no heat exchange and no work done, the change in internal energy (ΔU) is also zero:
ΔU=0
Thus, we have:
Q=0
Conclusion
The work done during the expansion is:
W=0
The heat during the expansion is:
Q=0
Final Answer
- Work Done (W) = 0
- Heat (Q) = 0
We have an insulated piston, which means that there is no heat exchange with the surroundings. The piston moves from an initial volume (V1) of 5 liters to a final volume (V2) of 10 liters.
The work done (W) during an expansion can be calculated using the formula:
W=−Pexternal×(V2−V1)
Where:
- Pexternal is the external pressure acting on the piston.
- V1 is the initial volume.
- V2 is the final volume.
Pexternal=0
Thus, substituting this into the work done formula:
W=−0×(10lit−5lit)=0
According to the first law of thermodynamics:
ΔU=Q+W
Where:
- ΔU is the change in internal energy.
- Q is the heat added to the system.
- W is the work done on the system.
ΔU=Q+0⇒ΔU=Q
In an insulated system, where there is no heat exchange and no work done, the change in internal energy (ΔU) is also zero:
ΔU=0
Thus, we have:
Q=0
The work done during the expansion is:
W=0
The heat during the expansion is:
Q=0
- Work Done (W) = 0
- Heat (Q) = 0
Topper's Solved these Questions
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - F-10
1 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - G-1
1 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - F-8
1 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
A sample of gas expands from volume V1 to V2. The amount of work done by the gas is greatest when the expansion is
View SolutionA gas expands from 75 liter to 125 liter at a constant pressure of 4 atmosphere. If one atmospheric pressure is 1.0x105Pa(Nm−2), calculate the work done by the gas during this expansion.
View SolutionA sample of an ideal gas is taken through the cyclic process abca . It absorbs 50 J of heat during the part ab, no heat during bc and rejects 70 J of heat during ca. 40 J of work is done on the gas during the part bc.(a) find the internal energy of the gas at b and c if it is 1500 J at a. (b) calculate the work done by the gas during the part ca.
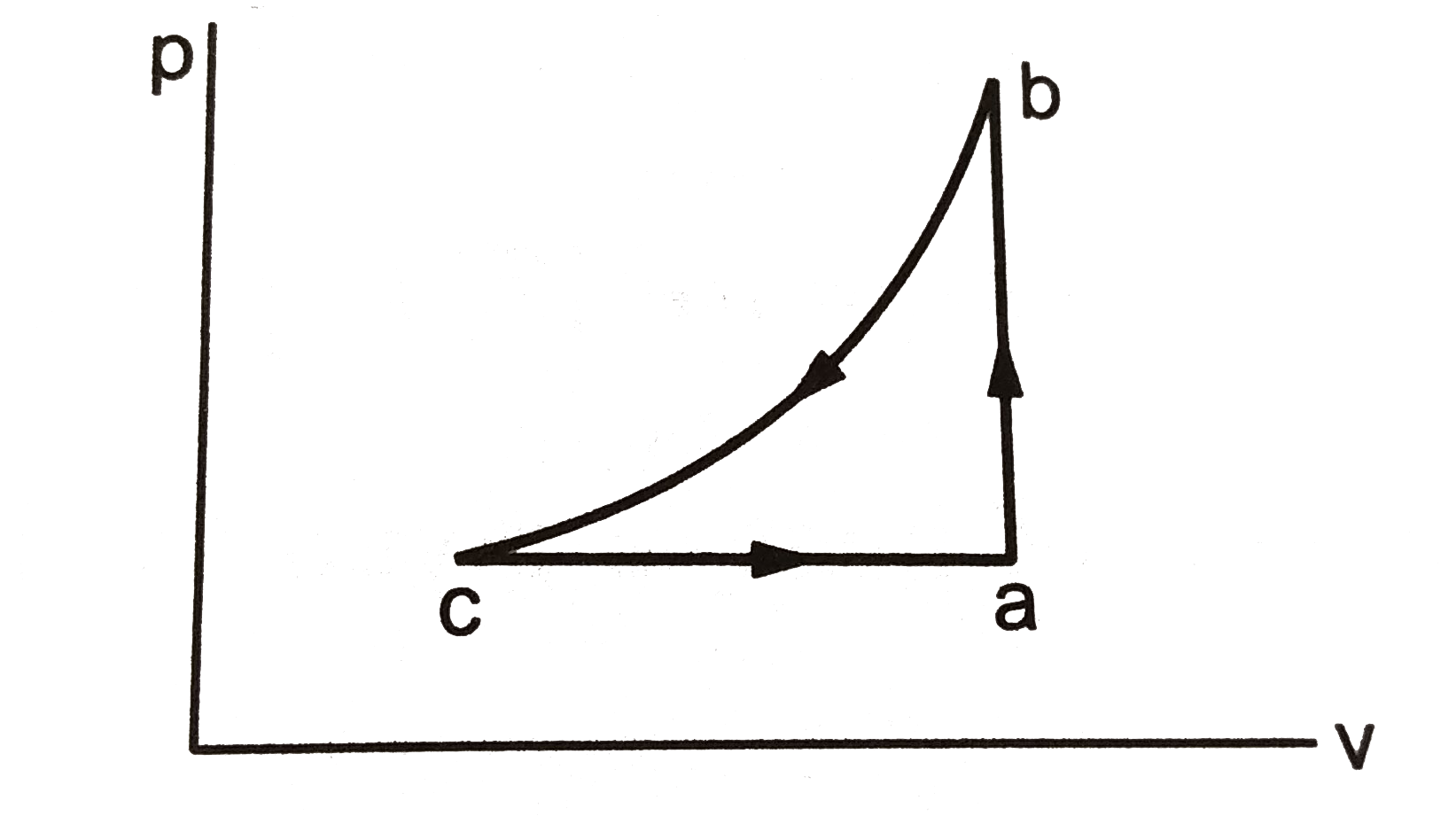
View SolutionA sample of an ideal gas is taken through the cyclic process abca . It absorbs 50J of heat during the part ab, no heat during bc and rejects 70J of heat during ca. 40J of work is done on the gas during the part bc.
(a) Find the internal energy of the gas at b and c if it is 1500J at a.
(b) Calculate the work done by the gas during the part ca.

View SolutionAn ideal gas is allowed to expand against a constant pressure of 2 bar from 10L to 50 L in one step. Calculate the amount of work done by the gas. If the same expansion were carried out reversibly, will the work done be higher or lower than the earlier case ?
(Give that, 1 L bar = 100 J)
View SolutionAn ideal gas of volume 1 litre and at a pressure 8 atm undergoes an adiabatic expansion until its pressure drops to 1 atm and volume increase to 4 liters. Calculate the work done in the process (y = 1.5).
View SolutionOne mole of oxygen is allowed to expand isothermally and reversibly from 5 m3 to 10 m3 at 300 K. Calculate the work done in expansion of the gas.
View SolutionOne mole of oxygen is allowed to expand isothermally and reversibly from 5 m3 to 10 m3 at 300 K. Calculate the work done in expansion of the gas.
View Solution1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.

View SolutionIn an isothermal reversible expansion, if the volume of 96 gm of oxygen at 27∘C is increased from 70 litres to 140 litres , then the work done by the gas will be
View Solution
