Consider a classroom that is roughly 5m×10m×3m. Initially T=27∘C and p=1 atm. There are 50 people in a insulated class losing energy to the room at the average rate of 150 Watt per person. How long can they remain in class if the body temperature is 42∘ C and person feels uncomfortable above this temperature. Heat capacity of air=(7/2)R
4.34 minutes
5.91 minutes
6.86 minutes
7.79 minutes
The correct Answer is:B
To solve the problem step by step, we will follow the given data and apply the relevant thermodynamic principles.
Step 1: Gather the Given Data
- Dimensions of the classroom: 5m×10m×3m
- Initial temperature of the room, Ti=27∘C
- Final uncomfortable temperature, Tf=42∘C
- Number of people, N=50
- Rate of energy loss per person, P=150W
- Heat capacity of air, Cp=72R
- Pressure, P=1atm
Step 2: Calculate the Volume of the Classroom
The volume V of the classroom can be calculated as:
V=5m×10m×3m=150m3
Step 3: Convert Volume to Liters
Since 1m3=1000L:
V=150m3×1000L/m3=150000L
Step 4: Calculate the Moles of Air in the Classroom
Using the Ideal Gas Law:
PV=nRT
Where:
- P=1atm=101.325kPa
- R=0.0821L⋅atm/(K⋅mol)
- T=27∘C+273.15=300.15K
Rearranging for n:
n=PVRT
Substituting the values:
n=(1atm)(150000L)(0.0821L⋅atm/(K⋅mol))(300.15K)≈6070.5mol
Step 5: Calculate the Heat Capacity of Air
Using the given heat capacity:
Cp=72R=72×8.314J/(mol⋅K)≈29.3J/(mol⋅K)
Step 6: Calculate the Total Heat Required to Raise the Temperature
The change in temperature ΔT is:
ΔT=Tf−Ti=42∘C−27∘C=15K
The total heat Q required is:
Q=n⋅Cp⋅ΔT
Substituting the values:
Q=6070.5mol⋅29.3J/(mol⋅K)⋅15K≈267,000J
Step 7: Calculate the Total Power Loss
The total power loss from all individuals is:
Ptotal=N⋅P=50⋅150W=7500W
Step 8: Calculate the Time to Reach Uncomfortable Temperature
Using the formula:
Q=Ptotal⋅t
Rearranging for t:
t=QPtotal=267000J7500W≈35.6s
Step 9: Convert Time to Minutes
To convert seconds to minutes:
t≈35.6s60≈0.593minutes
Final Answer
The time they can remain in the classroom before feeling uncomfortable is approximately 0.593 minutes.
- Dimensions of the classroom: 5m×10m×3m
- Initial temperature of the room, Ti=27∘C
- Final uncomfortable temperature, Tf=42∘C
- Number of people, N=50
- Rate of energy loss per person, P=150W
- Heat capacity of air, Cp=72R
- Pressure, P=1atm
The volume V of the classroom can be calculated as:
V=5m×10m×3m=150m3
Since 1m3=1000L:
V=150m3×1000L/m3=150000L
Using the Ideal Gas Law:
PV=nRT
Where:
- P=1atm=101.325kPa
- R=0.0821L⋅atm/(K⋅mol)
- T=27∘C+273.15=300.15K
n=PVRT
Substituting the values:
n=(1atm)(150000L)(0.0821L⋅atm/(K⋅mol))(300.15K)≈6070.5mol
Using the given heat capacity:
Cp=72R=72×8.314J/(mol⋅K)≈29.3J/(mol⋅K)
The change in temperature ΔT is:
ΔT=Tf−Ti=42∘C−27∘C=15K
The total heat Q required is:
Q=n⋅Cp⋅ΔT
Substituting the values:
Q=6070.5mol⋅29.3J/(mol⋅K)⋅15K≈267,000J
The total power loss from all individuals is:
Ptotal=N⋅P=50⋅150W=7500W
Using the formula:
Q=Ptotal⋅t
Rearranging for t:
t=QPtotal=267000J7500W≈35.6s
To convert seconds to minutes:
t≈35.6s60≈0.593minutes
The time they can remain in the classroom before feeling uncomfortable is approximately 0.593 minutes.
Topper's Solved these Questions
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise-2 II: Single and double value integer type
16 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise 2- III : One or more than one options correct type
14 Videos
- THERMODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise -1 Part -II Only option correct type
92 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
Consider a class room of dimensions 5×10×3m3 at atemperature 20∘C and pressure 1 atm. There are 50 people in the room, each losing energy at an average of 150 watt. Assuming that walls ceiling, floor and furniture are perfectly insulated and none of them absorb heat, what time (in seconds) will be needed for rising the temperature of air in the room to body temperature i.e., 37∘C? (For air CP=72R. Loss of air to outside as the temperature rises may be neglected).
View Solution50 students sitting in the room of 5×10×3m3 dimensions. The air inside the room is at 27∘C and 1atm pressure. If each student loses 100 watt heat per second assuming the walls, ceiling floor, and all the material present inside the room is perfectly insulated as well as neglecting loss of air to the outside as the temperature is raised, how much rise in temperature will be noticed in 10min? Given CP=72R for air.
View SolutionPhotosysthesis si a bio process by which plants make energy rich molecules from low energy molecules with the help of energy from sunlight . The photosysthesis of glucose can be represented as:
6CO2(g)+6H2Og+hv→C5H12O6(s)+6O2(g)..........(i)
The energy of one mole of a photon of wave lenght is known as one Einstein.
A glucose fuel cell was designed to generate 4000 Watts which was used to heat of 5m×5m×3m dimensions . The room is perfectly insulated and no heat flows out of the room Calculate the time needed to increase the temperature of the room by 20∘C , if the room was initially at 10∘C and 1 atm pressure . Assume that the air in the room behaves like an ideal gas and its molar heat capacity is 2.5R.
View SolutionImagine a system, that can keep the room temperature within a narrow range between 20∘C to 25∘C. The system includes a heat engine operating with variable power P = 3KT, where K is a constant coefficient, depending upon the thermal insulation of the room, the area of the walls and the thickness of the walls. T is temperature of the room in temperature drops lower than 20∘C, the engine turns on, when the temperature increase over 25∘C, the engine turns off, room looses energy at a rate of K(T−T0),T0 is the outdoor temperature. The heat capacity of the room is C.
Given (T0=10∘C,ln(32)=0.4,ln(65)=0.18,CK=750 SI-unit)
Suppose at t = 0, the engine turns off, after how much time interval, again, the engine will turn on
View SolutionImagine a system, that can keep the room temperature within a narrow range between 20∘C to 25∘C. The system includes a heat engine operating with variable power P = 3KT, where K is a constant coefficient, depending upon the thermal insulation of the room, the area of the walls and the thickness of the walls. T is temperature of the room in temperature drops lower than 20∘C, the engine turns on, when the temperature increase over 25∘C, the engine turns off, room looses energy at a rate of K(T−T0),T0 is the outdoor temperature. The heat capacity of the room is C.
Given (T0=10∘C,ln(32)=0.4,ln(65)=0.18,CK=750 SI-unit)
Suppose at t = 0, the engine turns on, after how much time interval again, the engine will turn off
View SolutionAn ideal gas expands from 100cm3→200cm3 at a constant pressure of 2.0×105 when 50J of heat is supplied to it. Calculate (a) the change in internal energy of the gas , (b) the number of moles in the gas if the initial temperature is 300K , (C ) the molar heat capacity CP at constant pressure and (d) the molar heat capacity Cv at constant volume
View SolutionThe glass windows of a room have a total area of 5m2 and glass thickness is 3mm. Calculate the rate at which heat escapes from the room per minute by conduction when the inside of the windows is at a temperature 15∘C and the outside temperature is −10∘C. Thermal conductivity =0.84Wm−1K−1.
View SolutionA metal block is placed in a room which is at 10∘C for long time. Now it is heated by an electric heater of power 500 W till its temperature becomes 50∘C. Its initial rate of rise of temperature is 2.5∘C/sec. The heater is switched off and now a heater of 100W is required to maintain the temperature of the block at 50∘C . (Assume Newtons Law of cooling to be valid)
What is the heat capacity of the block?
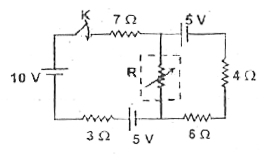
View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
View SolutionA room heater is made up of thin wall tubes of copper, each 1.0 m long and 4.0 cm in diameter. Hot water aet 77∘C circulates constantlyh through the tubes. Calculate the amount of heat radiated per second in a room where the average temperature is 27∘C. The emissivity of copper =0.8 and Stefan's contant =5.67×10−8Wm−2K−1
View Solution
