Cv value of He is always 3R/2 but Cv value of H2 is 3R/2 at low temperature and 5R/2 at moderate temperature and more than 5R/2 at higher temperature. Explain in two or three lines.
The correct Answer is:Hydrogen is diatomic so at high temperature rational and vibrational motion also counts.
Helium (He) gas is monoatomic and it has three translational degree of freedom. Hence, contribution of each transiational degree of freeedom towards Cv being R/2, so the total contribution towards Cv=3×R/2. Hydrogen molecule is diatomic. At low temperature, rotational and vibrational contribution for H2 are zero. So, Cv for H2 at low temperature continues to be 3R/2. At moderate temperature, rotational contribution (=2×R/2) also becomes dominant and hence total contribution towards Cv=3R2+R=5R2. At even high temperature, vibrational contribution (=1×R) also becomes significant. Hence total contibution towards Cv=3R2+R+R=7R2
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Main5videos
THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise-1 Part-I Subjective question30videos
THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Exercise-2 part -IV : Comprehension11videos
THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY50videos
TEST SERIES
Similar Questions
Cv values of He is always 3R2 but Cv values of H2 is 3R2
at low temperature and 5R2 at higher temperature explain .View SolutionThe molar heat capacity , Cv of helium gas is 3/2R and is independent of temperature. For hydrogen gas, Cv approaches 3/2R at very low temperature, equal 5/2R at moderate temperature and is higher than 5/2R at high temperatures. Give a reason for the temperature dependence of Cv in case of hydrogen, in not more than two or three sentences.
View SolutionA: H2 when allowed to expand at room temperature it causes heating effect.
R: H2 has inversion-temperature much below room temperature.View SolutionIn the circuit shown the resistance R is kept in a chamber whose temperature. is 20∘C which remains constant. The initial temperature and resistance of R is 50∘C and 15Ωrespectively. The rate of change of resistance R with temperature is 12Ω/∘C and the rate of decrease of temperature of R is In(3/100) times the temperature difference from the surrounding (Assume the resistance R loses heat only in accordance with Newton's law of cooling) If K is closed at t = 0, then find the
(a) value of. R for which power dissipation in it is maximum.
(b) temperature of R when power dissipation is maximum
(c) time after which the power dissipation will be maximum
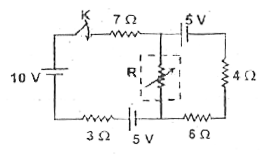 View Solution
View SolutionAt what temperature will He atoms have the same r.m.s. speed as H2 molecules have at 27∘C?
View SolutionResistance of a resistor at temperature t∘C is Rt=R0(1+αt+βt2), where R0 is the resistance at 0∘C. The temperature coefficient of resistance at temperature t∘C is
View SolutionTwo resistance R1 and R2 are made of different material. The temperature coefficient of the material of R1 is α and of the material of R2 is −β. Then resistance of the series combination of R1 and R2 will not change with temperature, if R1/R2 will not change with temperature if R1/R2 equals
View SolutionTwo resistance R1 and R2 are made of different material. The temperature coefficient of the material of R1 is α and of the material of R2 is −β. Then resistance of the series combination of R1 and R2 will not change with temperature, if R1/R2 will not change with temperature if R1/R2 equals
View Solution1 mole of an ideal gas A (Cv,m=3R) and 2 mole of an ideal gas B are (Cv.m=32R) taken in a constainer and expanded reversible and adiabatically from 1 litre of 4 litre starting from initial temperature of 320K. ΔEorΔU for the process is (in Cal)
View Solution1 mole of an ideal gas A(Cv.m=3R) and 2 mole of an ideal gas B are (Cv,m=32R) taken in a container and expanded reversible and adiabatically from 1 litre of 4 litre starting from initial temperature of 320 K. ΔE or ΔU for the process is :
View Solution

