Entropy is a state function and its value depends on two or three variable temperature (T), Pressure(P) and volume (V). Entropy change for an ideal gas having number of moles(n) can be determined by the following equation.
Since free energy change for a process or a chemical equation is a deciding factor of spontaneity , which can be obtained by using entropy change according to the expression, at a temperature
For a reaction and atm. Calculate upto which temperature the reaction would not be spontaneous.
K
K
K
K
The correct Answer is:D
To determine the temperature up to which the reaction M2O(s)→2M(s)+12O2(g) would not be spontaneous, we will use the Gibbs free energy equation:
ΔG=ΔH−TΔS
Step 1: Understand the spontaneity condition
A reaction is spontaneous when ΔG<0. Therefore, for the reaction to be non-spontaneous, we need:
ΔG≥0
This leads us to the condition:
ΔH−TΔS≥0
Step 2: Rearranging the equation
Rearranging the equation gives us:
ΔH≥TΔS
From this, we can express the temperature T:
T≤ΔHΔS
Step 3: Substitute the given values
We know from the problem:
- ΔH=30kJ/mol=30,000J/mol (since we need to convert kJ to J)
- ΔS=0.07kJ/mol=70J/mol
Now we substitute these values into the equation:
T≤30,000J/mol70J/mol
Step 4: Calculate the temperature
Calculating the right-hand side:
T≤30,00070≈428.57K
Step 5: Conclusion
Thus, the reaction would not be spontaneous at temperatures greater than approximately 428.57K. Therefore, the temperature up to which the reaction would not be spontaneous is:
T<428.57K
A reaction is spontaneous when ΔG<0. Therefore, for the reaction to be non-spontaneous, we need:
Rearranging the equation gives us:
We know from the problem:
- ΔS=0.07kJ/mol=70J/mol
Calculating the right-hand side:
Thus, the reaction would not be spontaneous at temperatures greater than approximately 428.57K. Therefore, the temperature up to which the reaction would not be spontaneous is:
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - exercise-3 Part:(I)23videos
THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - exercise-3 part-1 Advanced level Solutions30videos
THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - exercise-2 Part:(III): One or more than one options correct8videos
THERMODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - CHEMISTRY50videos
TEST SERIES
Similar Questions
Entropy is a state function and its value depends on two or three variable temperature (T), Pressure(P) and volume (V). Entropy change for an ideal gas having number of moles(n) can be determined by the following equation.
ΔS=2.303nCvlog(T2T1)+2.303nR log(V2V1)
ΔS=2.303nCPlog(T2T1)+2.303nR log(P1P2)
Since free energy change for a process or a chemical equation is a deciding factor of spontaneity , which can be obtained by using entropy change (ΔS) according to the expression, ΔG=ΔH−TΔS at a temperature T
What would be the entropy change involved in thermodynamic expansion of 2 moles of a gas from a volume of 5 L to a volume of 50 L at 25∘ C [Given R=8.3J/mole−K]View SolutionEntropy is a state function and its value depends on two or three variable temperature (T), Pressure(P) and volume (V). Entropy change for an ideal gas having number of moles(n) can be determined by the following equation.
ΔS=2.303nCvlog(T2T1)+2.303nR log(V2V1)
ΔS=2.303nCPlog(T2T1)+2.303nR log(P1P2)
Since free energy change for a process or a chemical equation is a deciding factor of spontaneity , which can be obtained by using entropy change (ΔS) according to the expression, ΔG=ΔH−TΔS at a temperature T
An isobaric process having one mole of ideal gas has entropy change 23.03 J/K for the temperature range 27∘ C to 327∘ C . What would be the molar specific heat capacity (Cv)?View SolutionIf Kc is not numerically equal to Kp, how can both of the following equations be valid?
ΔGɵ=−2.303RTlogKc,ΔGɵ=−2.303RTlogKpView SolutionFor V versus T curves at constant pressure P1andP2 for an ideal gas are shown in the figure given below
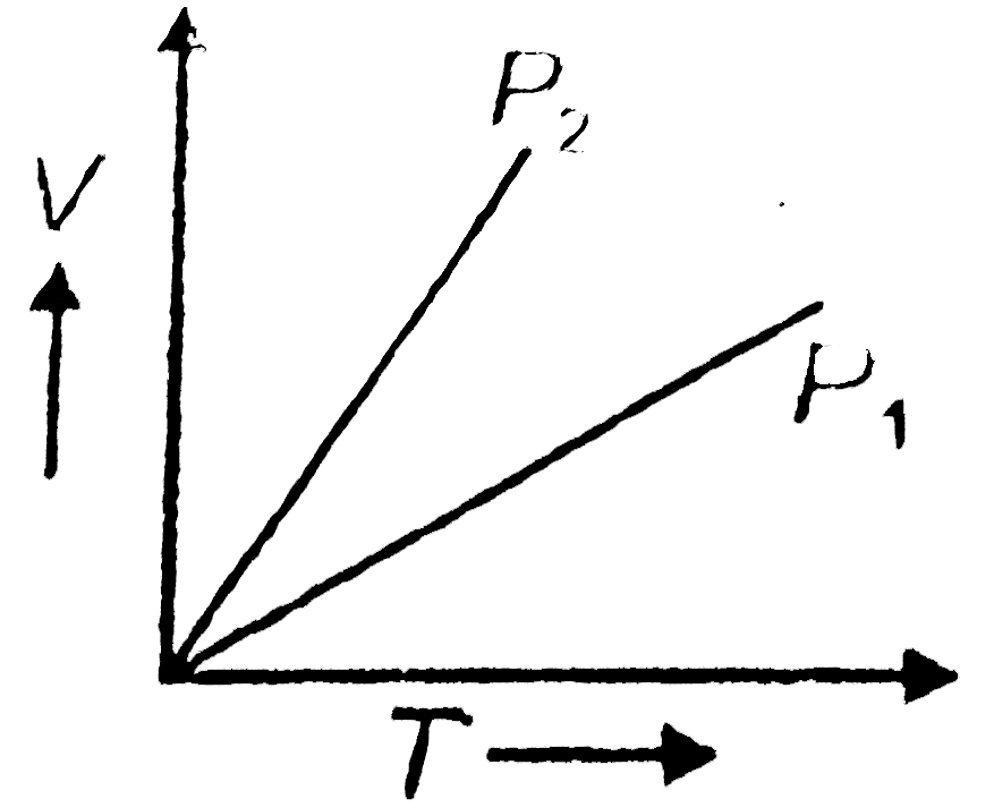 View Solution
View SolutionV vs T curves at constant pressure P1 and P2 for an ideal gas are shown below
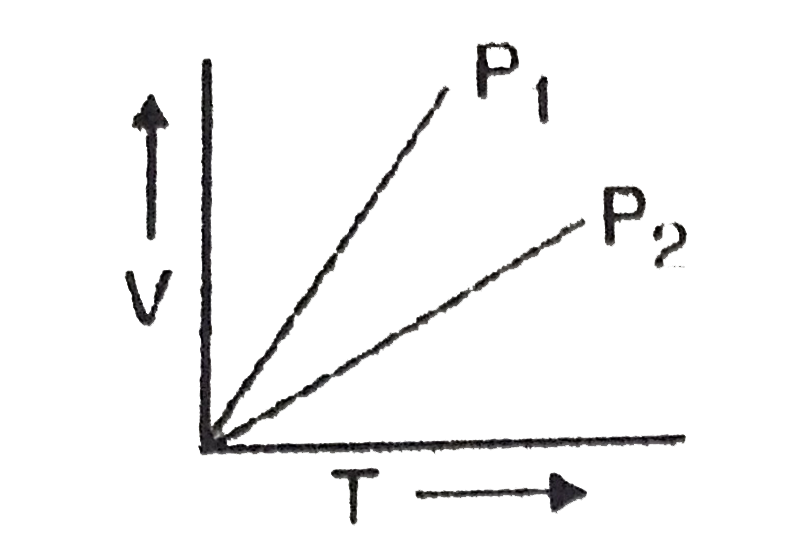
Which is correct ?View SolutionFor a sample of n mole of a perfect gas at constant temperature T (K) when its volume is changed from V1 to V2 the entropy change is given by
View SolutionFor V versus T curves at constant pressure P1andP2 for and ideal gas shown in figure-
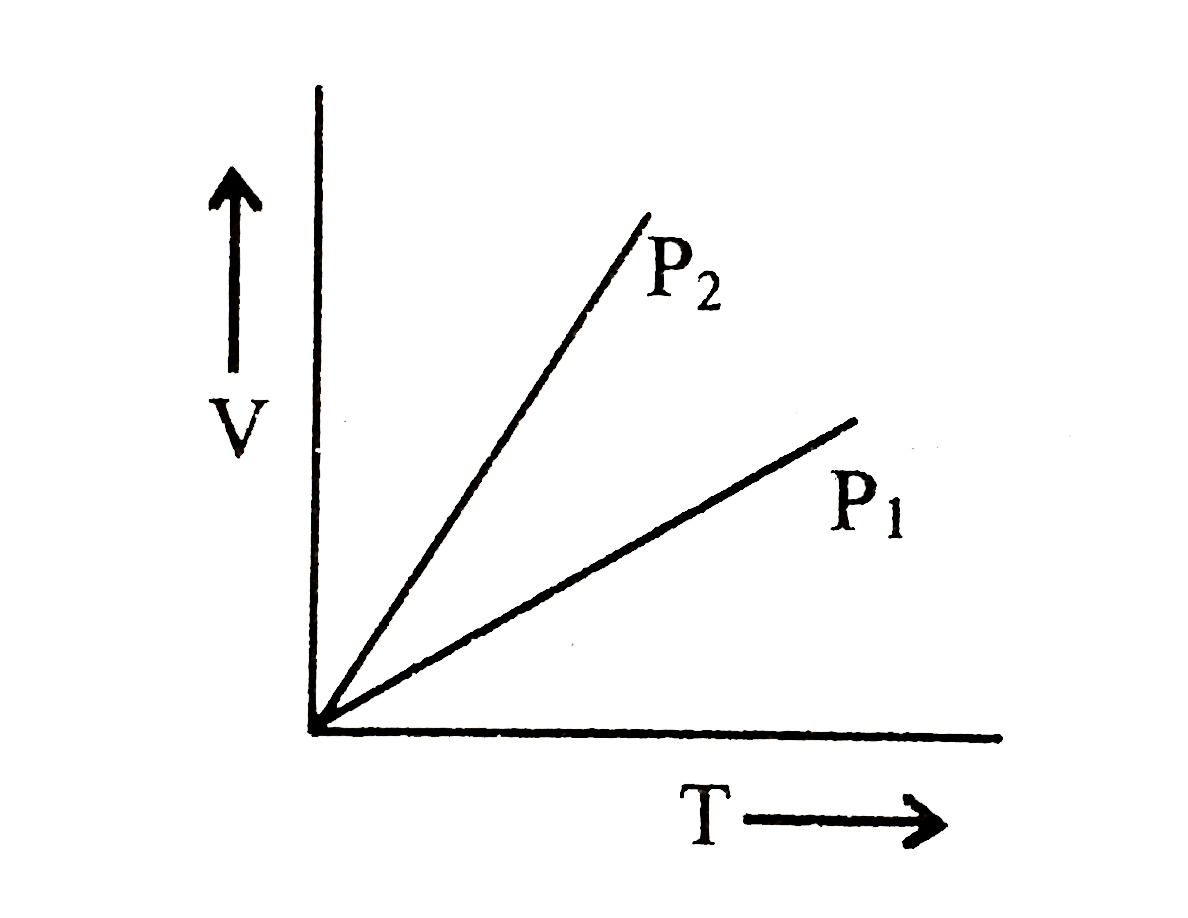 View Solution
View SolutionFigure shows volume - temperature (V-T) graph for same mass of an ideal gas at two different pressures P1and P2. Hence
View SolutionA plot of P vs T for a given mass of gas at constant volume is a straight line . P vs T at constant volumes V1 and V2 for an ideal gas are shown below :
Which of the following is correct ?
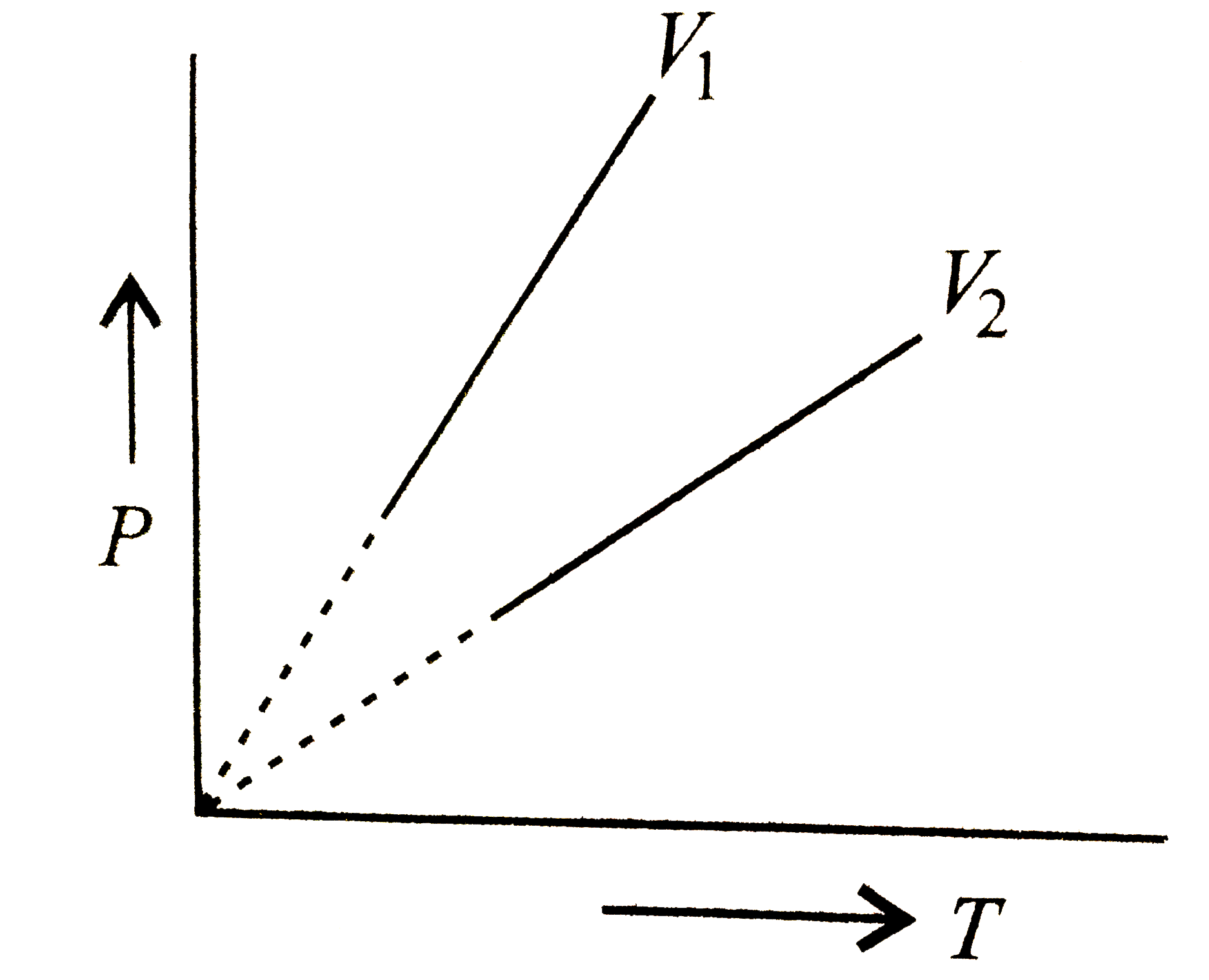 View Solution
View SolutionThe equation of state of a real gas is given by (P+aV2)(V−b)=RT
where P, V and T are pressure, volume and temperature resperature and R is the universal gas constant. The dimensions of the constant a in the above equation isView Solution

