ΔG is the available energy (energy produced) during the electochemical reaction in galvanic cell which can be converted into useful work. In the light of second law of thermodynamics, in the cell, the change in electrode potential with temperature will be equal to:
△SnF
nF△S
−2.303RTlogKC
−2.303nF
The correct Answer is:A
To solve the problem regarding the change in electrode potential with temperature in a galvanic cell, we can follow these steps:
Step 1: Understand the relationship between Gibbs free energy and electrode potential
In electrochemistry, the Gibbs free energy change (ΔG) is related to the electrode potential (E) of a galvanic cell by the equation:
ΔG=−nFE
where:
- ΔG is the change in Gibbs free energy,
- n is the number of moles of electrons transferred,
- F is Faraday's constant (approximately 96485 C/mol),
- E is the electrode potential.
Step 2: Apply the second law of thermodynamics
According to the second law of thermodynamics, the change in entropy (ΔS) is related to the change in Gibbs free energy and temperature (T) by the equation:
ΔG=ΔH−TΔS
For a spontaneous process in a galvanic cell, ΔG is negative, and we can express the change in Gibbs free energy in terms of temperature and entropy.
Step 3: Differentiate the Gibbs free energy equation with respect to temperature
To find the change in electrode potential with temperature, we differentiate the equation for ΔG with respect to temperature (T):
d(ΔG)dT=−nFdEdT
Step 4: Relate the change in Gibbs free energy to entropy
From the thermodynamic identity, we know that:
ΔS=−d(ΔG)dT
Substituting this into our differentiated equation gives:
−nFdEdT=−ΔS
Step 5: Solve for the change in electrode potential with temperature
Rearranging the equation to solve for dEdT:
dEdT=ΔSnF
Final Answer
Thus, the change in electrode potential with temperature in a galvanic cell is given by:
dEdT=ΔSnF
In electrochemistry, the Gibbs free energy change (ΔG) is related to the electrode potential (E) of a galvanic cell by the equation:
- ΔG is the change in Gibbs free energy,
- n is the number of moles of electrons transferred,
- F is Faraday's constant (approximately 96485 C/mol),
- E is the electrode potential.
According to the second law of thermodynamics, the change in entropy (ΔS) is related to the change in Gibbs free energy and temperature (T) by the equation:
To find the change in electrode potential with temperature, we differentiate the equation for ΔG with respect to temperature (T):
From the thermodynamic identity, we know that:
Rearranging the equation to solve for dEdT:
Thus, the change in electrode potential with temperature in a galvanic cell is given by:
Topper's Solved these Questions
- ELECTROCHEMISRYBOOK - RESONANCE ENGLISHCHAPTER - ELECTROCHEMISRYEXERCISE - Comprehension
30 Videos
- ELECTROCHEMISRYBOOK - RESONANCE ENGLISHCHAPTER - ELECTROCHEMISRYEXERCISE - Exercise 3
7 Videos
- ELECTROCHEMISRYBOOK - RESONANCE ENGLISHCHAPTER - ELECTROCHEMISRYEXERCISE - Subjective Questions
14 Videos
- ELECTRO CHEMISTRYBOOK - RESONANCE ENGLISHCHAPTER - ELECTRO CHEMISTRYEXERCISE - PHYSICAL CHEMITRY (ELECTROCHEMISTRY)
53 Videos
- EQUIVALENT CONCEPT & TITRATIONSBOOK - RESONANCE ENGLISHCHAPTER - EQUIVALENT CONCEPT & TITRATIONSEXERCISE - Part -IV
22 Videos
Similar Questions
The emf of a galvanic cell is positive when free energy change of reaction is
View SolutionIn which of the following cell the energy of combustion of the reaction is directly converted into electricity?
View SolutionGalvanic cells generate electrical energy at the expense of a spontaneous redox reaction. In an electrode concentration cell two like electrodes having different concentrations, either because they are gas electrodes operating at different pressures or because they are amalgams (solutions in mercury) with different concentrations are dipped into the same solution.
Eg. An example is a cell composed of two chlorine electrodes with different pressure of Cl2:
PtL|Cl2(PL)|HCl(aq)|Cl2(PR)|PtR
Where PL and PR are the Cl2 pressure at the left and right electrodes.
Calculate the EMF of the electrode concentration cell represented by :
Hg−Zn(c1)∣∣Zn+2(aq)∣∣Hg−Zn(c2)
At 25∘C.c1=2g of Zn per 100g of Hg and c2=1g of Zn per 50g of Hg
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
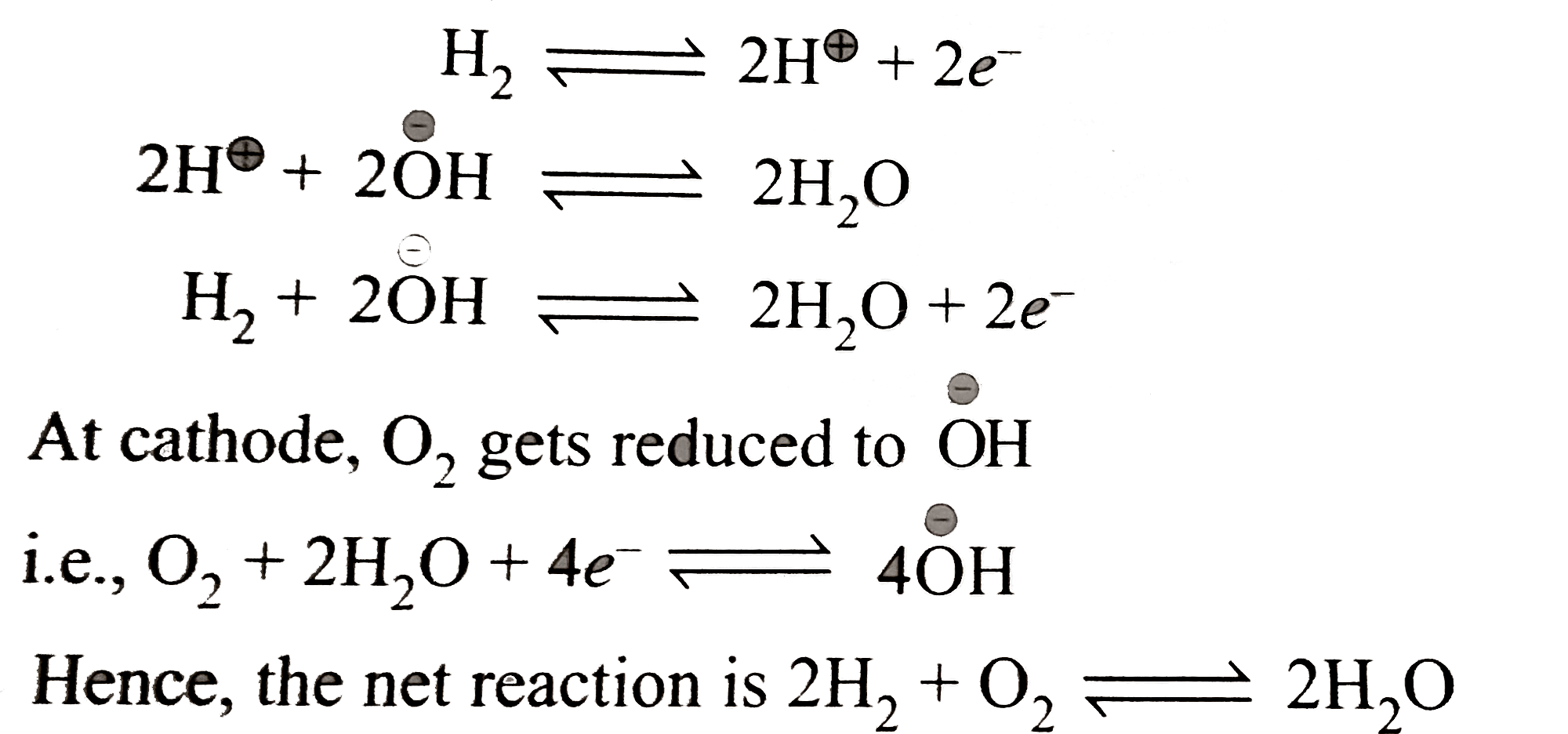
At cathode, O2 gets reduced to c−OH
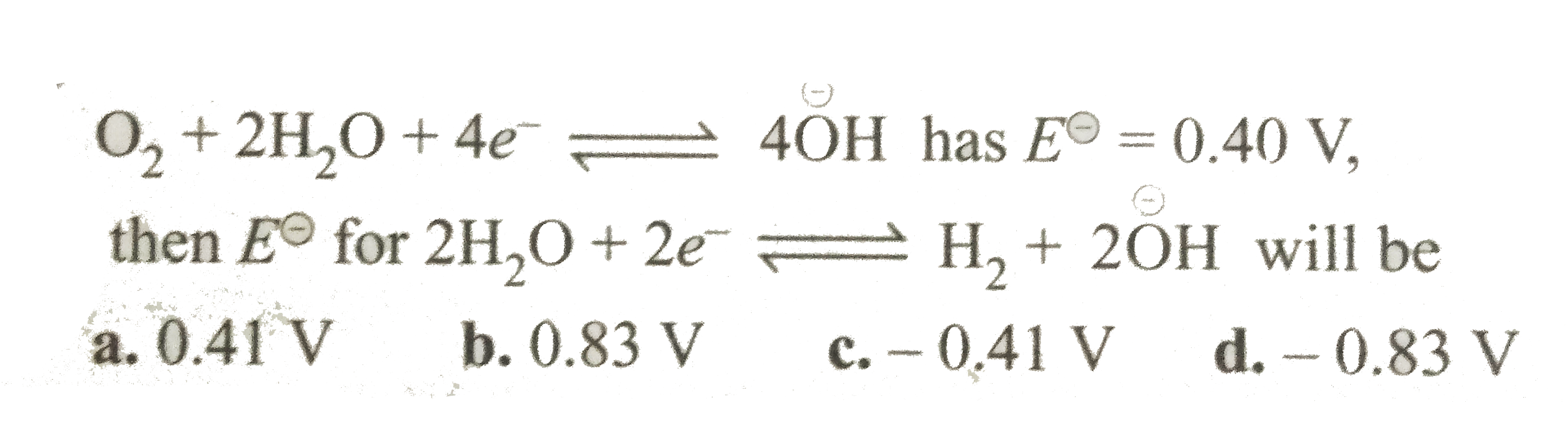
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
If the cell voltage is 1.23V for the H2−O2 fuel cell and for the half cell :
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
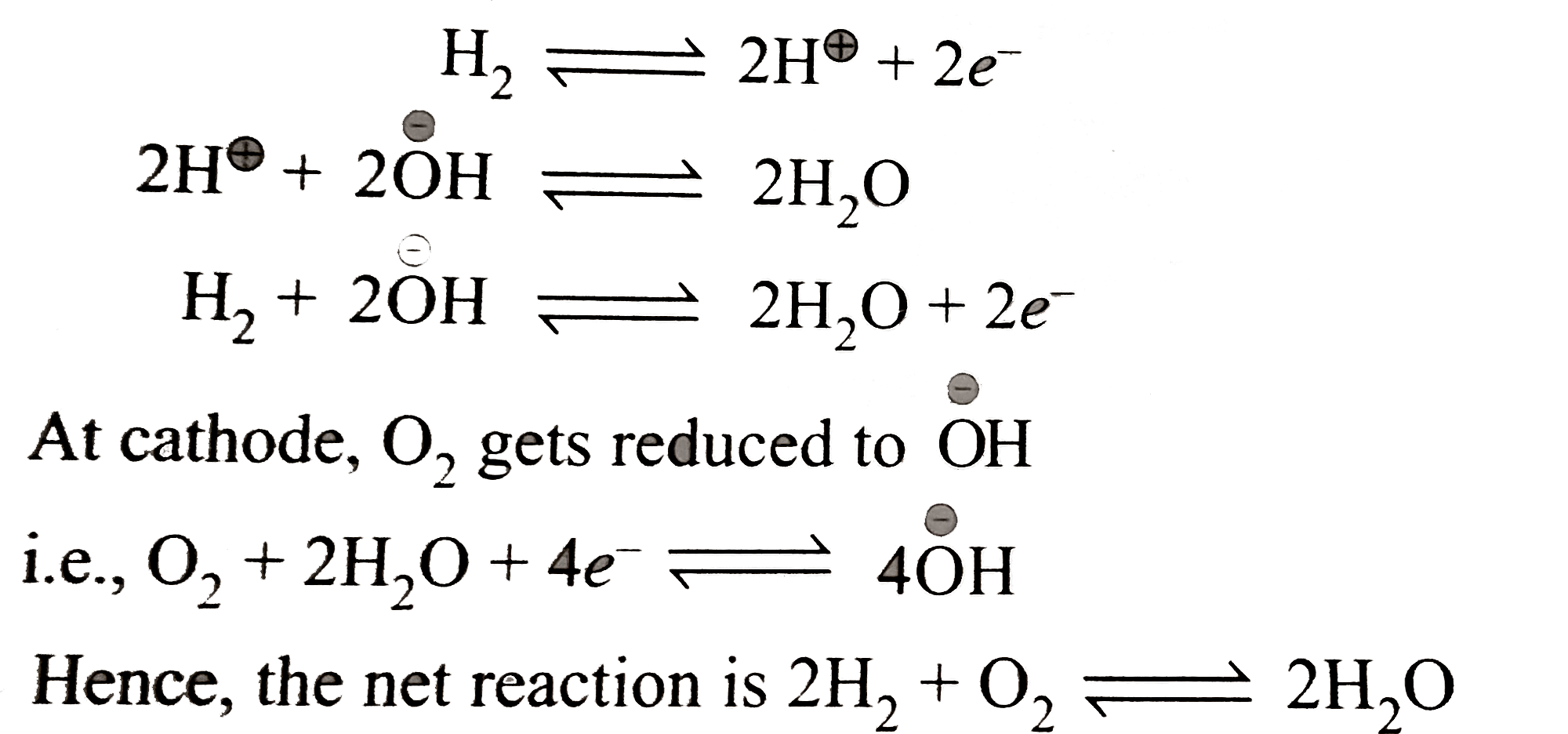
At cathode, O2 gets reduced to c−OH
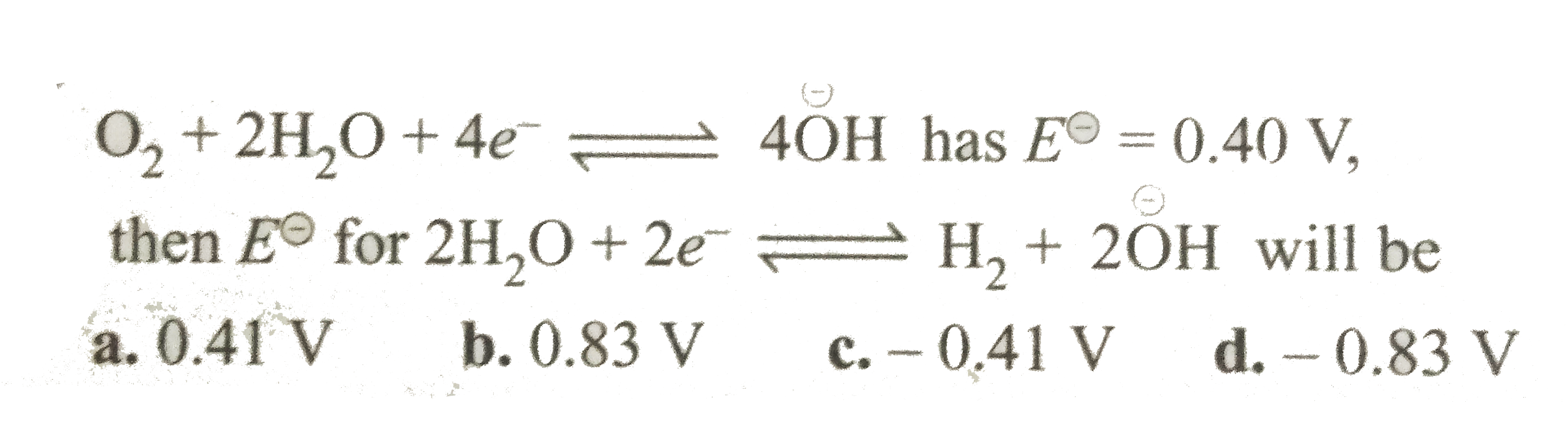
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
If the cell voltage is 1.23V for the H2−O2 fuel cell and for the half cell :
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
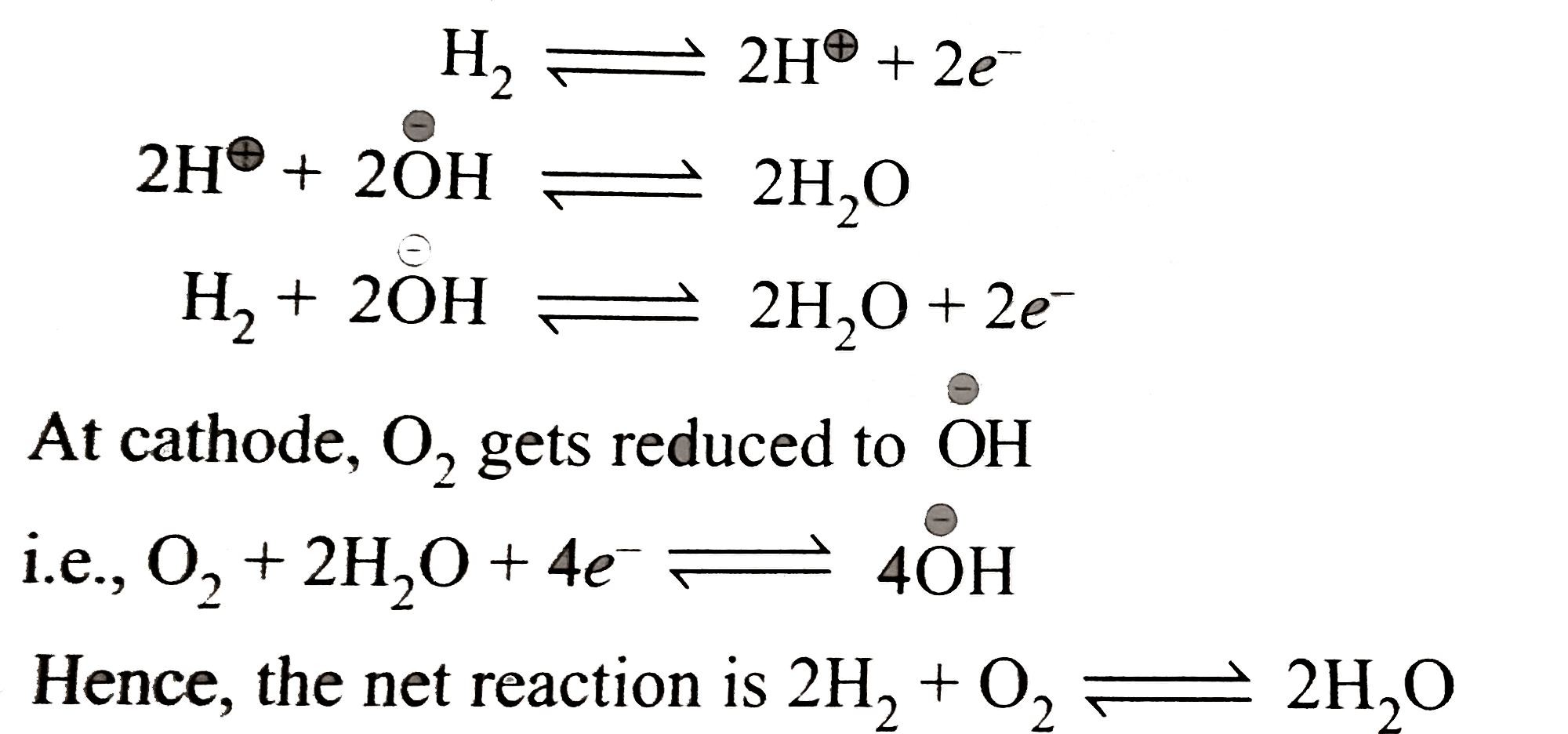
At cathode, O2 gets reduced to c−OH
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
Suppose the concentration of hydroxide ioin in the cell is doubled, then the cell voltage will be
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
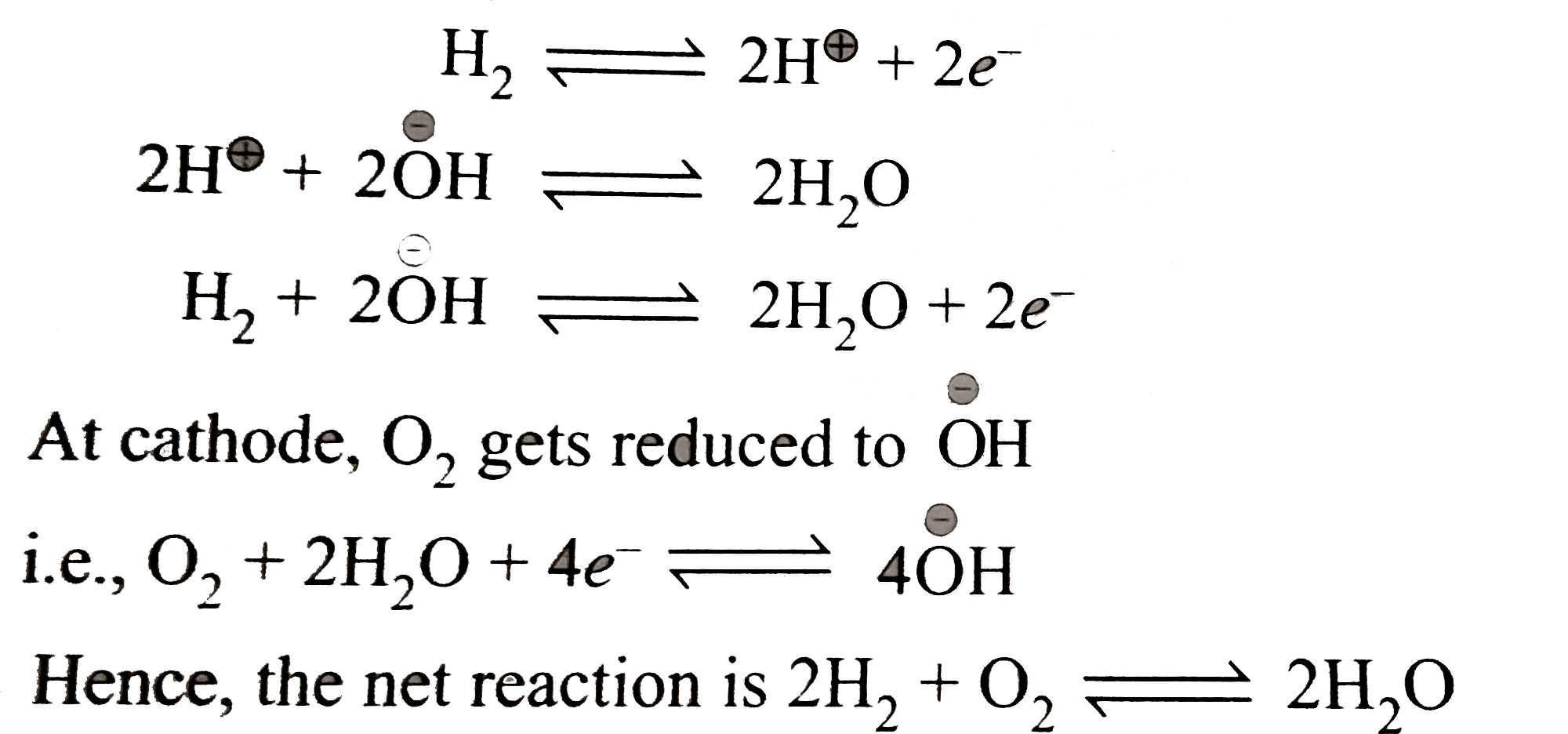
At cathode, O2 gets reduced to c−OH
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
What is the value of ΔSc− for the fuel cell at 25∘C?
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
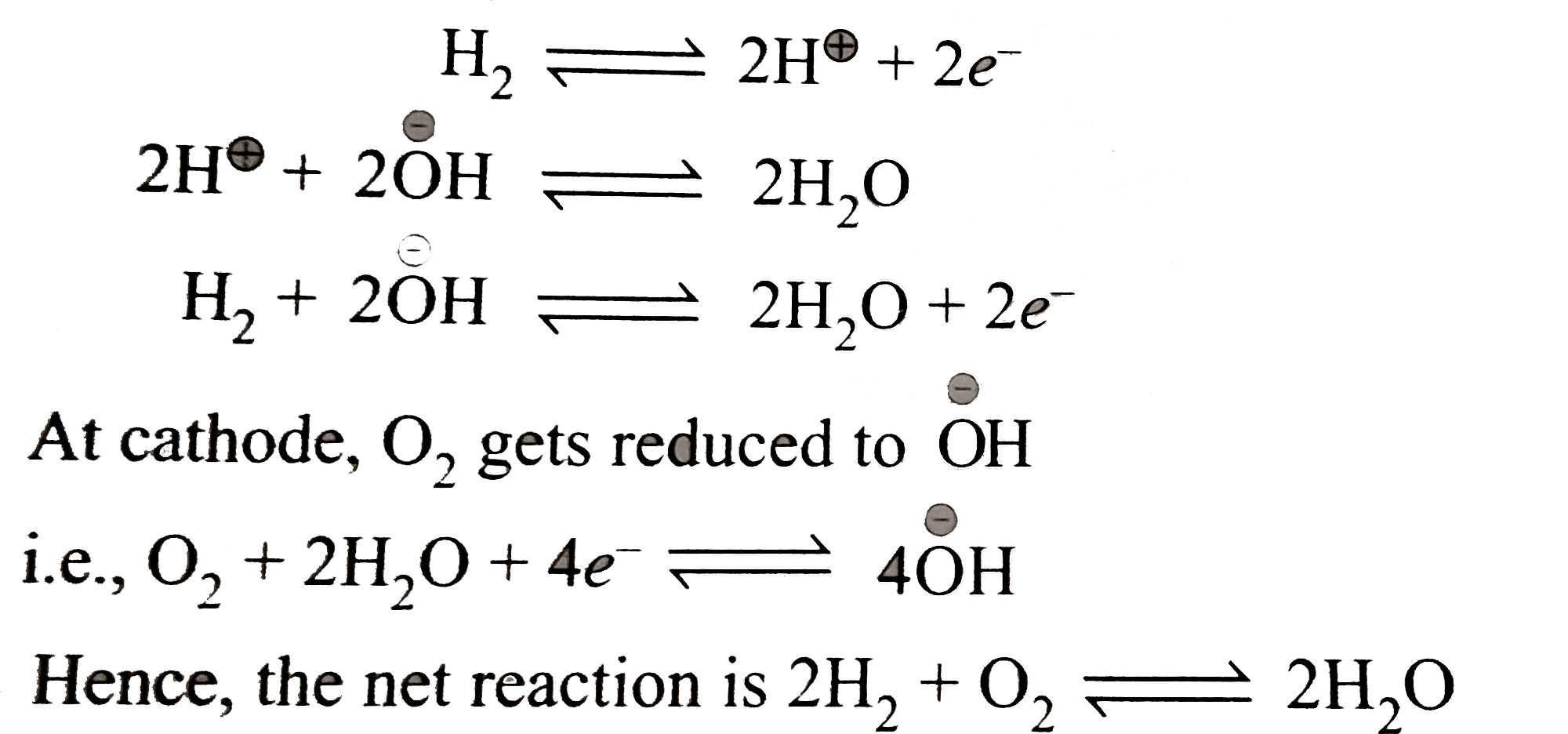
At cathode, O2 gets reduced to c−OH
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
What is the value of ΔSc− for the fuel cell at 25∘C?
a.−1600JK−1
b.−160JK−1
c.160JK−1
d.1600JK−1
View SolutionFuel cells : Fuel cells are galvanic cells in which the chemical energy of fuel cell is directly converted into electrical energy. A type of fuel cell is a hydrogen − oxygen fuel cell. It consists of two electrodes made up of two porous graphite impregnated with a catalyst ( platinum, silver, or metal oxide ). The electrodes are placed in aqueous solution of NaOH . Oxygen and hydrogen are continuously fed into the cell. Hydrogen gets oxidized to H⊕ which is neutralized by c−OH,i.e., anodic reaction.
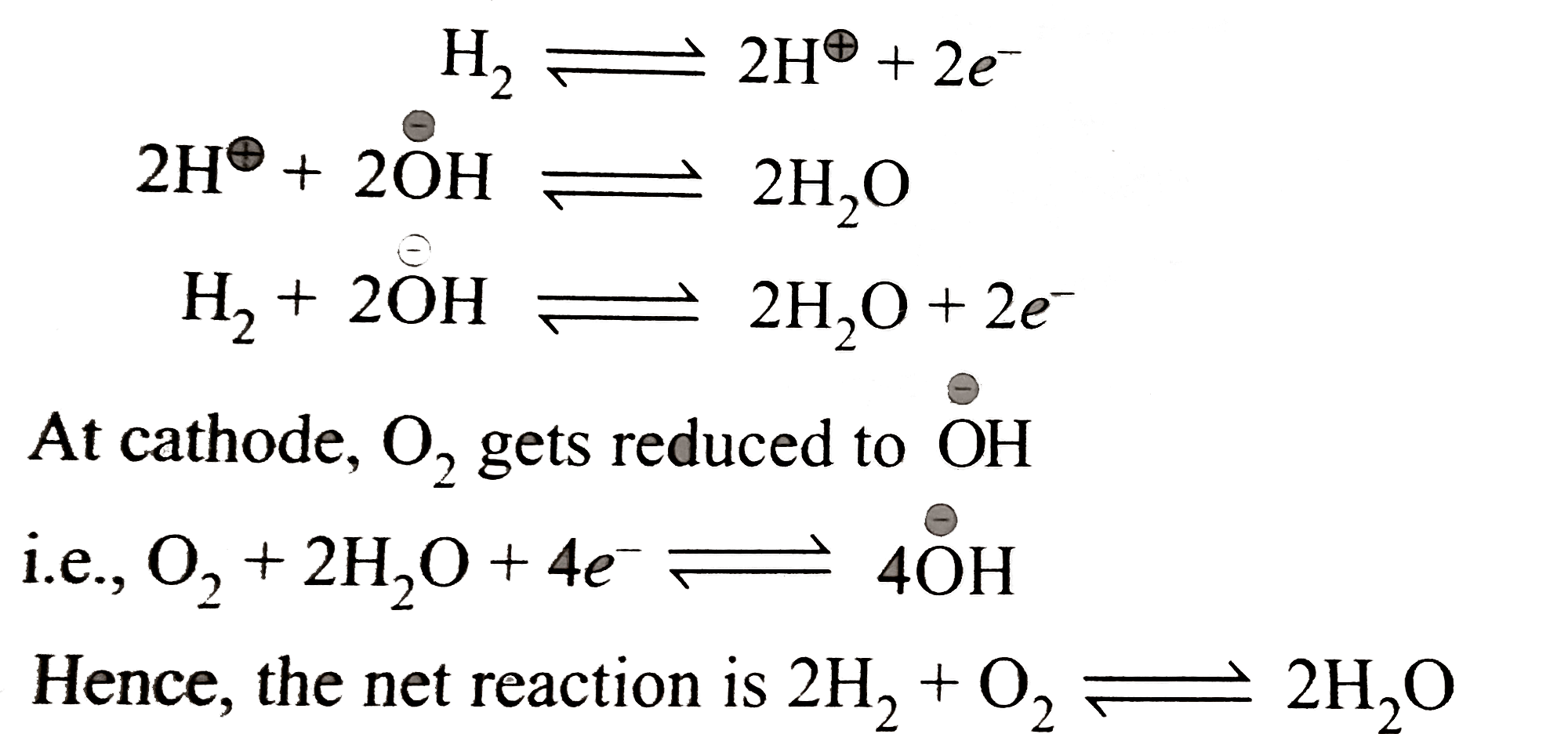
At cathode, O2 gets reduced to c−OH
Hence, the net reaction is
The overall reaction has
ΔH=−285.6kJmol−1 and ΔG=−237.4kJmol−1 at 25∘C
A fuel cell is
I. A voltaic cell in which continuous supply of fuels are sent at anode to perform oxidation.
II. A voltaci cell in which fuels such as :CH4,H2, and CO are used up at anode.
III. One which involves the reaction of H2−O2 fuel cell such as :
Anode :2H2O+4c−OH→4H2O(l)+4ec−
Cathode :O2+2H2O(l)=4e−→4c−OH
IV. The efficiency of H2−O20 fuel cell is 70 to 75%
View SolutionChemical reactions are invariably associated with the transfer of energy either in the form of hear or light. In the laboratory, heat changes in physical and chemical processes are measured with an instrument called calorimeter. Heat change in the process is calculated as: q= ms ΔT, s= Specific heat = cΔT= Heat capacity. Heat of reaction at constant pressure is measured using simple or water calorimeter. Qv=ΔU= Internal energy change, QP=ΔH,QP=QV+PΔVandΔH=ΔU+ΔnRT. The amount of energy released during a chemical change depends on the physical state of reactants and products, the condition of pressure, temperature and volume at which the reaction is carried out. The variation of heat of reaction with temperature and pressure is given by Kirchoff's equation: ΔH2−ΔH1T2−T1=ΔCP (At constant pressure), ΔU2−ΔU1T2−T1=ΔCV (At constant volume)
The enthalpy change (ΔH) for the reaction N2(g)+3H2(g)→2NH3(g) is −92.38kJ at 298 K. The internal energy change ΔU at 298 K is
View Solution