Effect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
For exothermic reaction if ΔS∘<0 then the sketch of log k vs 1T may be
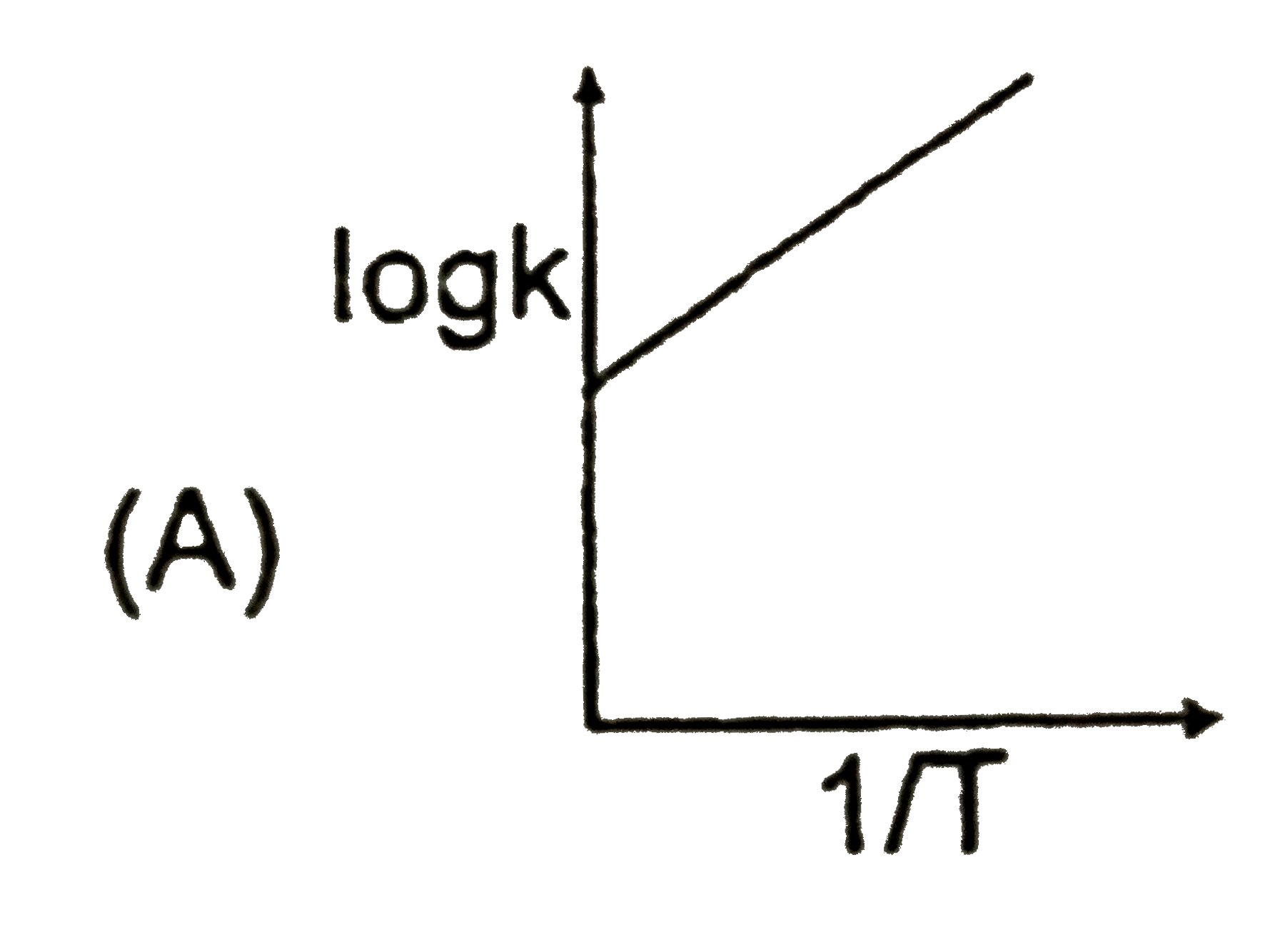


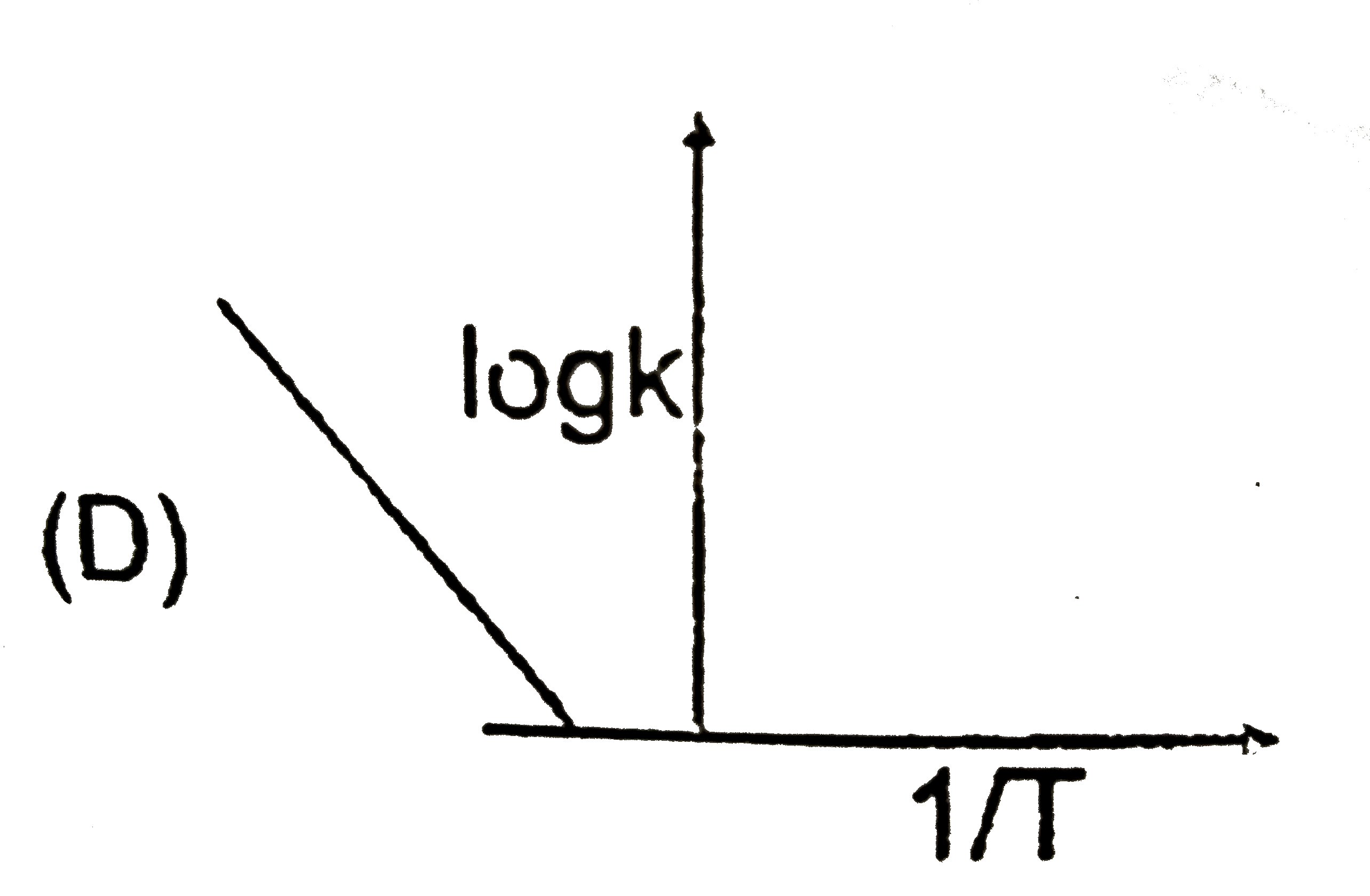
The correct Answer is:B
To analyze the effect of temperature on the equilibrium constant using thermodynamics, we can follow these steps:
Step 1: Understand the Relationship Between Gibbs Free Energy and Equilibrium Constant
The Gibbs free energy change (ΔG°) for a reaction is related to the equilibrium constant (K) by the equation:
ΔG(@)=−2.303RTlogK
This equation shows that the Gibbs free energy change is directly related to the logarithm of the equilibrium constant.
Step 2: Relate Gibbs Free Energy to Enthalpy and Entropy
The Gibbs free energy change can also be expressed in terms of enthalpy (ΔH°) and entropy (ΔS°) changes:
ΔG(@)=ΔH(@)−TΔS(@)
This equation indicates that the change in Gibbs free energy is influenced by both the enthalpy change and the temperature multiplied by the entropy change.
Step 3: Combine the Two Equations
By equating the two expressions for ΔG°:
−2.303RTlogK=ΔH(@)−TΔS(@)
Rearranging gives:
logK=−ΔH(@)2.303RT+ΔS(@)2.303R
This equation shows how the equilibrium constant K varies with temperature (T).
Step 4: Analyze the Slope and Intercept
If we plot log K versus 1T, we can identify the slope and intercept:
- The slope (m) is given by:
m=−ΔH(@)2.303R
- The y-intercept (c) is:
c=ΔS(@)2.303R
For an exothermic reaction, ΔH° is negative, which means the slope will be positive.
Step 5: Consider the Sign of ΔS°
If ΔS° is negative, the intercept will also be negative. Thus, we expect a graph where:
- The slope is positive (due to negative ΔH°).
- The intercept is negative (due to negative ΔS°).
Step 6: Conclusion
From the analysis, we conclude that for an exothermic reaction with ΔS° < 0, the plot of log K versus 1T will show a positive slope and a negative intercept.
The Gibbs free energy change (ΔG°) for a reaction is related to the equilibrium constant (K) by the equation:
ΔG(@)=−2.303RTlogK
This equation shows that the Gibbs free energy change is directly related to the logarithm of the equilibrium constant.
The Gibbs free energy change can also be expressed in terms of enthalpy (ΔH°) and entropy (ΔS°) changes:
ΔG(@)=ΔH(@)−TΔS(@)
This equation indicates that the change in Gibbs free energy is influenced by both the enthalpy change and the temperature multiplied by the entropy change.
By equating the two expressions for ΔG°:
−2.303RTlogK=ΔH(@)−TΔS(@)
Rearranging gives:
logK=−ΔH(@)2.303RT+ΔS(@)2.303R
This equation shows how the equilibrium constant K varies with temperature (T).
If we plot log K versus 1T, we can identify the slope and intercept:
- The slope (m) is given by:
m=−ΔH(@)2.303R
- The y-intercept (c) is:
c=ΔS(@)2.303R
For an exothermic reaction, ΔH° is negative, which means the slope will be positive.
If ΔS° is negative, the intercept will also be negative. Thus, we expect a graph where:
- The slope is positive (due to negative ΔH°).
- The intercept is negative (due to negative ΔS°).
From the analysis, we conclude that for an exothermic reaction with ΔS° < 0, the plot of log K versus 1T will show a positive slope and a negative intercept.
Topper's Solved these Questions
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-3 (Part-1)
6 Videos
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-3 (Part-2)
17 Videos
- CHEMICAL EQUILIBRIUMBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL EQUILIBRIUMEXERCISE - Exercise-2 (Part-3)
33 Videos
- CHEMICAL BONDINGBOOK - RESONANCE ENGLISHCHAPTER - CHEMICAL BONDINGEXERCISE - ORGANIC CHEMISTRY(Fundamental Concept )
6 Videos
- D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS BOOK - RESONANCE ENGLISHCHAPTER - D & F-BLOCK ELEMENTS & THEIR IMPORTANT COMPOUNDS EXERCISE - Match the column
1 Videos
Similar Questions
At constant temperature , the equilibrium constant (KP) for the decomposition reaction
N2O4⇔2NO2, is expressed by Kp=(4x2p)(1−x2)
where p= pressure ,x = extent of decomposition .which one of the following statements is true?
View SolutionIn which of the following equilibrium ,change in volume of the system does not alter the number of moles:
View SolutionWhich of the following is correct about the chemical equilibrium ?
View SolutionThe correct order of dipole moment is .
View SolutionCuSO4 reacts with NH3 to give blue complex of
View SolutionΔG=ΔH−TΔS and ltBRgt ΔG=ΔH+T[d(ΔG)dT]p, then(dEcelldT) is
View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
If statndard heat of dissociation of PCl5 is 230 cal then slope of the graph of log vs 1T is :
View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
For exothermic reaction if ΔS∘<0 then the sketch of log k vs 1T may be
View SolutionEffect of temperature on the equilibrium process analysed by using the thermodynamics
From the thermodynamics reaction
ΔG∘=−2.30RTlogk
ΔG∘: Standing free energy change
ΔG∘=ΔH∘−TΔS∘…(ii)
ΔH∘:Standard heat of the reaction gt
From eqns.(i) and(ii)
−2RTlogk=ΔH∘=TΔS∘
ΔS∘ : standard entropy change
⇒ logK=−ΔH∘2.3RT+ΔS∘2.3R
Clearly, if a plot of k vs 1/T is made then it is a straight lone having slope =−ΔH∘2.3R amd y intercept =ΔS∘2.3R
If at temperature T1 equilibrium constant be k1 and at temperature T2equilibrium constant be k2 then :
⇒ logK1=−ΔH∘2.3RT1+ΔS∘2.3R..(iv)
⇒ logK2=−ΔH∘2.3RT2+ΔS∘2.3R...(v)
Substracting e.q (iv) from (v), we get
from the relation we can conclude that the of equilibrium constant increase in temperature for endothermic reaction eith but value of equilibrium constant decrease with the increase in temperature for exothermic reaction
If for a particular reversible reaction
KC=57 abd 355∘C and KC=69 at 450∘C then
View SolutionThe relation ΔG=ΔH−TΔS was given by
View Solutionसमीकरण ΔG=ΔH−TΔS की व्युत्पत्ति कीजिए ।
View SolutionFor a process at a particular temperature and pressure, DeltaG=DeltaH-TDeltaS . It can be written as: -DeltaG=T[-(DeltaH)/(T)+DeltaS] . What does the quantity within the bracket indicate?
View SolutionIf DeltaG=DeltaH-TDeltaS and DeltaG = DeltaH+T[(d(DeltaG))/(dT)] , then variation EMF of a cell E, with temperature T, is given by
View SolutionThe relation ΔG=ΔH−TΔS was given by
View SolutionΔG=ΔH−TδSandΔG=ΔH+T[d(ΔG)dT] then (dEcelldT) is
View SolutionEstablish DeltaG = DeltaH- TDeltaS .
View Solution
