Illustrate an octahedral void in the close packing of spheres. Why is it so called ?
The correct Answer is:Octahedral void is present at the body center, which is formed by six face centered atoms and it consist at triangle faces
To illustrate an octahedral void in the close packing of spheres, we can follow these steps:
1. Understanding Close Packing of Spheres:
- In a close packing arrangement, spheres (representing atoms) are packed together in a way that maximizes their density. The two most common types of close packing are face-centered cubic (FCC) and hexagonal close packing (HCP).
2. Visualizing the Arrangement:
- Imagine arranging spheres in layers. Start with a layer of spheres in a triangular arrangement. This layer will be the base layer.
3. Adding the Second Layer:
- Place a second layer of spheres above the first layer. The spheres in this layer will fit into the depressions formed by the spheres in the first layer.
4. Identifying the Octahedral Void:
- The octahedral void is formed at the center of the arrangement where the spheres from the first and second layers meet. In a simple representation, if you have three spheres forming a triangle in one layer, and three spheres directly above them in the second layer, the space in the center of this arrangement is the octahedral void.
5. Counting the Surrounding Atoms:
- An octahedral void is surrounded by six spheres: three above the void and three below it. This gives it a coordination number of six, which is characteristic of octahedral geometry.
6. Naming the Void:
- It is called an "octahedral void" because of its geometric shape, which resembles an octahedron. The void is defined by the six surrounding spheres, creating a space that can be visualized as an octahedron.
Summary:
An octahedral void in the close packing of spheres is formed by the arrangement of spheres where six spheres surround a central void, three above and three below. This is why it is referred to as an octahedral void, reflecting its geometric properties and coordination number.
- In a close packing arrangement, spheres (representing atoms) are packed together in a way that maximizes their density. The two most common types of close packing are face-centered cubic (FCC) and hexagonal close packing (HCP).
- Imagine arranging spheres in layers. Start with a layer of spheres in a triangular arrangement. This layer will be the base layer.
- Place a second layer of spheres above the first layer. The spheres in this layer will fit into the depressions formed by the spheres in the first layer.
- The octahedral void is formed at the center of the arrangement where the spheres from the first and second layers meet. In a simple representation, if you have three spheres forming a triangle in one layer, and three spheres directly above them in the second layer, the space in the center of this arrangement is the octahedral void.
- An octahedral void is surrounded by six spheres: three above the void and three below it. This gives it a coordination number of six, which is characteristic of octahedral geometry.
- It is called an "octahedral void" because of its geometric shape, which resembles an octahedron. The void is defined by the six surrounding spheres, creating a space that can be visualized as an octahedron.
An octahedral void in the close packing of spheres is formed by the arrangement of spheres where six spheres surround a central void, three above and three below. This is why it is referred to as an octahedral void, reflecting its geometric properties and coordination number.
Topper's Solved these Questions
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Part-II : Only one option correct type
42 Videos
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercise -2 (Part-I)
19 Videos
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Miscellaneous solved problems
16 Videos
- S BLOCK ELEMENTSBOOK - RESONANCE ENGLISHCHAPTER - S BLOCK ELEMENTSEXERCISE - ORGANIC CHEMISTRY(Biomolecules & Polymer)
4 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBOOK - RESONANCE ENGLISHCHAPTER - STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYEXERCISE - Section -B
18 Videos
Similar Questions
Knowledge Check
Assertion:A tetrahedral void is surrounded by four spheres and an octahedral void is surrounded by six spheres.
Reason:The number of tetrahedral voids is double the number of close packed spheres and number of octahedral voids is equal to number of close packed spheres.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false
In octahedral holes (voids):
View SolutionThe number of octahedral sites in a cubical close pack array of N spheres is
View SolutionHow many octahedral & tetrahedral voids are per sphere in a unit cell ?
View SolutionVolume occupied for a cubic close packed lattice of sphere is
View SolutionThe number of octahedral voids in case of hcp unit cell is
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
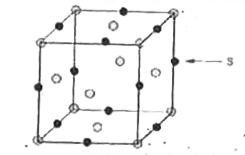
View Solution
