A student wants to arrange 4 identical spheres (of radiusR) on a two dimensional floor as close as possible. Finally he could arrange them. Identify the type and dimensions of the figure obtained by joining their centers. Could he occupy the whole available space, if not, then what type of voids were generated. Calculate their number and radius of small ball that can be fitted in them.
The correct Answer is:No, Rhombous: 2R, 60º,120º; Triangular voids; 2 voids, 0.155 R
To solve the problem of arranging four identical spheres of radius R on a two-dimensional floor as close as possible, we can follow these steps:
Step 1: Arrangement of Spheres
To arrange four identical spheres as close as possible, we can position them in a square formation. The centers of the spheres will form the vertices of a square.
Step 2: Identify the Figure
When we join the centers of the four spheres, we obtain a square. The dimensions of the square can be determined as follows:
- The distance between the centers of two adjacent spheres is equal to 2R (since the radius of each sphere is R).
- Therefore, the side length of the square formed by the centers is 2R.
Step 3: Space Occupation
Next, we need to determine if the spheres occupy the whole available space. Since the spheres are arranged in a square, they do not occupy the entire area of the square. There will be some unoccupied space.
Step 4: Identify the Type of Voids
The unoccupied space between the spheres can be identified as voids. In this arrangement, the voids formed are triangular voids. Specifically, there are two triangular voids formed at the corners of the square.
Step 5: Calculate the Number of Voids
In total, there are two triangular voids formed in this arrangement.
Step 6: Calculate the Radius of Small Balls that can Fit in the Voids
To calculate the radius of the small ball that can fit into the triangular voids, we can use the known ratio for triangular voids. The radius r of the small ball that can fit in a triangular void is given by:
r≈0.155R
Summary of Results
- Type of Figure: Square
- Dimensions of Figure: Side length = 2R
- Type of Voids: Triangular voids
- Number of Voids: 2
- Radius of Small Ball that can Fit in Voids: r≈0.155R
To arrange four identical spheres as close as possible, we can position them in a square formation. The centers of the spheres will form the vertices of a square.
When we join the centers of the four spheres, we obtain a square. The dimensions of the square can be determined as follows:
- The distance between the centers of two adjacent spheres is equal to 2R (since the radius of each sphere is R).
- Therefore, the side length of the square formed by the centers is 2R.
Next, we need to determine if the spheres occupy the whole available space. Since the spheres are arranged in a square, they do not occupy the entire area of the square. There will be some unoccupied space.
The unoccupied space between the spheres can be identified as voids. In this arrangement, the voids formed are triangular voids. Specifically, there are two triangular voids formed at the corners of the square.
In total, there are two triangular voids formed in this arrangement.
To calculate the radius of the small ball that can fit into the triangular voids, we can use the known ratio for triangular voids. The radius r of the small ball that can fit in a triangular void is given by:
r≈0.155R
- Type of Figure: Square
- Dimensions of Figure: Side length = 2R
- Type of Voids: Triangular voids
- Number of Voids: 2
- Radius of Small Ball that can Fit in Voids: r≈0.155R
Topper's Solved these Questions
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Part-II : Only one option correct type
42 Videos
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercise -2 (Part-I)
19 Videos
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Miscellaneous solved problems
16 Videos
- S BLOCK ELEMENTSBOOK - RESONANCE ENGLISHCHAPTER - S BLOCK ELEMENTSEXERCISE - ORGANIC CHEMISTRY(Biomolecules & Polymer)
4 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBOOK - RESONANCE ENGLISHCHAPTER - STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYEXERCISE - Section -B
18 Videos
Similar Questions
Which of the following is/are pseudo solids?
(P) KCl
(Q) Barium chloride dihydrate
(C ) Coke left after distillation of coal tar:
View SolutionWhich of the following are not correctly matched with the bonds found between the constituents particle?
View SolutionCalculate the number of fornula units in each of the following types of unit cells:
(a) MgO in a rock salt type unit cell
(b) ZnS in zinc blende structure
(c) platinum in a face-centred cubic unit cell
View SolutionS2: Plaster of paris is a hemihydrate of calcium sulphate obtained by heating the gypsum above 393K.
S2: Sodium carbonate is used in water softening.
S4: The order of mobilities of the alkali metal ions in aqueous solutions is Li+>Na+>K+>Rb+>Cs+
View SolutionIn Kjeldahl's method, nitrogen present is estimated as
View SolutionYou are given 6 identical balls. What is the maximum number of square voids and triangular voids ( in separate arrangements) that can be created?
View SolutionPacking refers to the arrangement of constituent units in such a way that the forces of attraction among the constituent particles is the maximum and the contituents occupy the maximum available space. In two dimensions, there are hexagonal close packing and cubic close packing. In three dimentions, there are hexagonal, cubic as well as body centred close packings.
The space occupied by spheres in bcc arrangement is:
View SolutionA student wants to arrange 4 identical spheres (of radiusR) on a two dimensional floor as close as possible. Finally he could arrange them. Identify the type and dimensions of the figure obtained by joining their centers. Could he occupy the whole available space, if not, then what type of voids were generated. Calculate their number and radius of small ball that can be fitted in them.
View SolutionYou are given 4 identical balls. What is the maximum number of square voids and triangular voids (in separate arrangements) that can be created ?
View SolutionYou are given 6 identical balls. What is the maximum number of square voids and triangular voids (in separate arrangements) that can be created ?
View SolutionThe available space occupied by spheres of equal size in three dimensions in both hcp and ccp arrangement is
View SolutionHow many type of holes are generated in a hexagonal and a cubic close-packed arrangement of identical spheres?
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
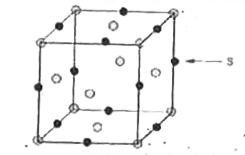
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
If the anions (A) form hexagonal close packing and cations (C ) occupy only 2/3rd octahedral voids in it, then the general formula of the compound is
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View Solution
