In which of the following arrangments octahedral voids are formed ?
hcp
bcc
simple cubic
fcc
The correct Answer is:A, D
Step by step video & image solution for In which of the following arrangments octahedral voids are formed ? by Chemistry experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercise -2 (Part-IV Comprehension)
8 Videos
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercise -3 (Part-I)
16 Videos
- SOLID STATEBOOK - RESONANCE ENGLISHCHAPTER - SOLID STATEEXERCISE - Exercise -2 (Part-II Single correct double value integer type)
9 Videos
- S BLOCK ELEMENTSBOOK - RESONANCE ENGLISHCHAPTER - S BLOCK ELEMENTSEXERCISE - ORGANIC CHEMISTRY(Biomolecules & Polymer)
4 Videos
- STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYBOOK - RESONANCE ENGLISHCHAPTER - STRUCTURAL IDENTIFICATION & PRACTICAL ORGANIC CHEMISTRYEXERCISE - Section -B
18 Videos
Similar Questions
Knowledge Check
Which of the following statements is not about the voids ?
AOctahedral void is formed at the centre of six spheres which lies at the apices of a regular octahedronBThere is one octahedral site for each sphereCThere are two tetrahedral sites for each sphereDOctahedral voids are formed when the triangular voids in second layer exactly overlap with similar voids in the first layer .
Which of the following represent octahedral void ?
View SolutionWhich of the following is not true about the voids formed in 3 dimensional hexagonal close packed structure?
View SolutionWhat is the coordination number of octahedral voids?
View SolutionIn octahedral holes (voids):
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In the figure given below, the site marked as S is a
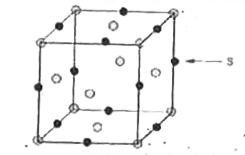
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
Mark the false statement :
View SolutionIn HCP or CCP constituent particles occupy 74% of the available space. The remaining space (26%) in between the spheres remains unoccupied and is called interstitial voids or holes. Considering the close packing arrangement, each sphere in the second layer rests on the hollow space of the first layer, touching each other. The void created is called tetrahedral void. If R is the radius of the spheres in the close packed arrangement then,
R (radius of tetrahedral void) = 0.225 R
In a close packing arrangement, the interstitial void formed by the combination of two triangular voids of the first and second layer is called octahedral coid. Thus, double triangular void is surrounded by six spheres. The centre of these spheres on joining, forms octahedron. If R is the radius of the sphere. in a close packed arrangement then,
R (radius of octahedral void = 0.414 R).
In Schottky defect
View Solution
