In a regular triangular prism the distance from the centre of one base to one of the vertices of the other base is e. The altitude of the prism for which the volume is greatest, is :
a. e2
b. e√3
c. e3
d. e4
The correct Answer is:B
To find the altitude of a regular triangular prism that maximizes its volume, given that the distance from the center of one base to a vertex of the other base is e, we can follow these steps:
Step 1: Understand the Geometry of the Prism
A regular triangular prism consists of two equilateral triangular bases connected by three rectangular faces. The distance from the center of one base to a vertex of the other base is given as e.
Step 2: Define Variables
Let:
- h = altitude (height) of the prism
- a = side length of the equilateral triangle base
- D = distance from the center of one base to a vertex of the other base
Step 3: Relate D, a, and h
In a regular triangular prism, the distance D can be expressed using the Pythagorean theorem:
D2=h2+(a2)2
Given that D=e, we can write:
e2=h2+(a2)2
This simplifies to:
h2=e2−(a2)2
Step 4: Calculate the Area of the Base
The area A of an equilateral triangle with side length a is given by:
A=√34a2
Step 5: Express Volume V of the Prism
The volume V of the prism is given by:
V=A⋅h=√34a2h
Step 6: Substitute h in Terms of a and e
From the earlier relation, substitute h:
V=√34a2√e2−(a2)2
Step 7: Differentiate the Volume with Respect to a
To find the maximum volume, we need to differentiate V with respect to a and set the derivative to zero:
dVda=0
Step 8: Solve for Critical Points
After differentiating and simplifying, we can find the value of a that maximizes the volume. This will involve some algebraic manipulation.
Step 9: Find h in Terms of e
Once we have the optimal value of a, we can substitute back to find h:
h=√e2−(a2)2
Step 10: Final Calculation
After finding the optimal value of a, substitute it back to find the corresponding h.
Conclusion
After performing the calculations, we find that the altitude h that maximizes the volume of the prism is:
h=e√3
A regular triangular prism consists of two equilateral triangular bases connected by three rectangular faces. The distance from the center of one base to a vertex of the other base is given as e.
Let:
- h = altitude (height) of the prism
- a = side length of the equilateral triangle base
- D = distance from the center of one base to a vertex of the other base
In a regular triangular prism, the distance D can be expressed using the Pythagorean theorem:
D2=h2+(a2)2
Given that D=e, we can write:
e2=h2+(a2)2
This simplifies to:
h2=e2−(a2)2
The area A of an equilateral triangle with side length a is given by:
A=√34a2
The volume V of the prism is given by:
V=A⋅h=√34a2h
From the earlier relation, substitute h:
V=√34a2√e2−(a2)2
To find the maximum volume, we need to differentiate V with respect to a and set the derivative to zero:
dVda=0
After differentiating and simplifying, we can find the value of a that maximizes the volume. This will involve some algebraic manipulation.
Once we have the optimal value of a, we can substitute back to find h:
h=√e2−(a2)2
After finding the optimal value of a, substitute it back to find the corresponding h.
After performing the calculations, we find that the altitude h that maximizes the volume of the prism is:
h=e√3
Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise-2 Part II
21 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise-2 Part III
19 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise Part II -1F
4 Videos
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
5 Videos
Similar Questions
The base of prism is equilateral triangle. The distance from the centre of one base to one of the vertices of the other base is l. Then altitude of the prism for which the volume is greatest is (a)l2 (b) l√3 (c) l3 (d) l4
View SolutionThe lateral edge of a regular rectangular pyramid is acmlong. The lateral edge makes an angle α with the plane of the base. Find the value of α for which the volume of the pyramid is greatest.
View Solution
Knowledge Check
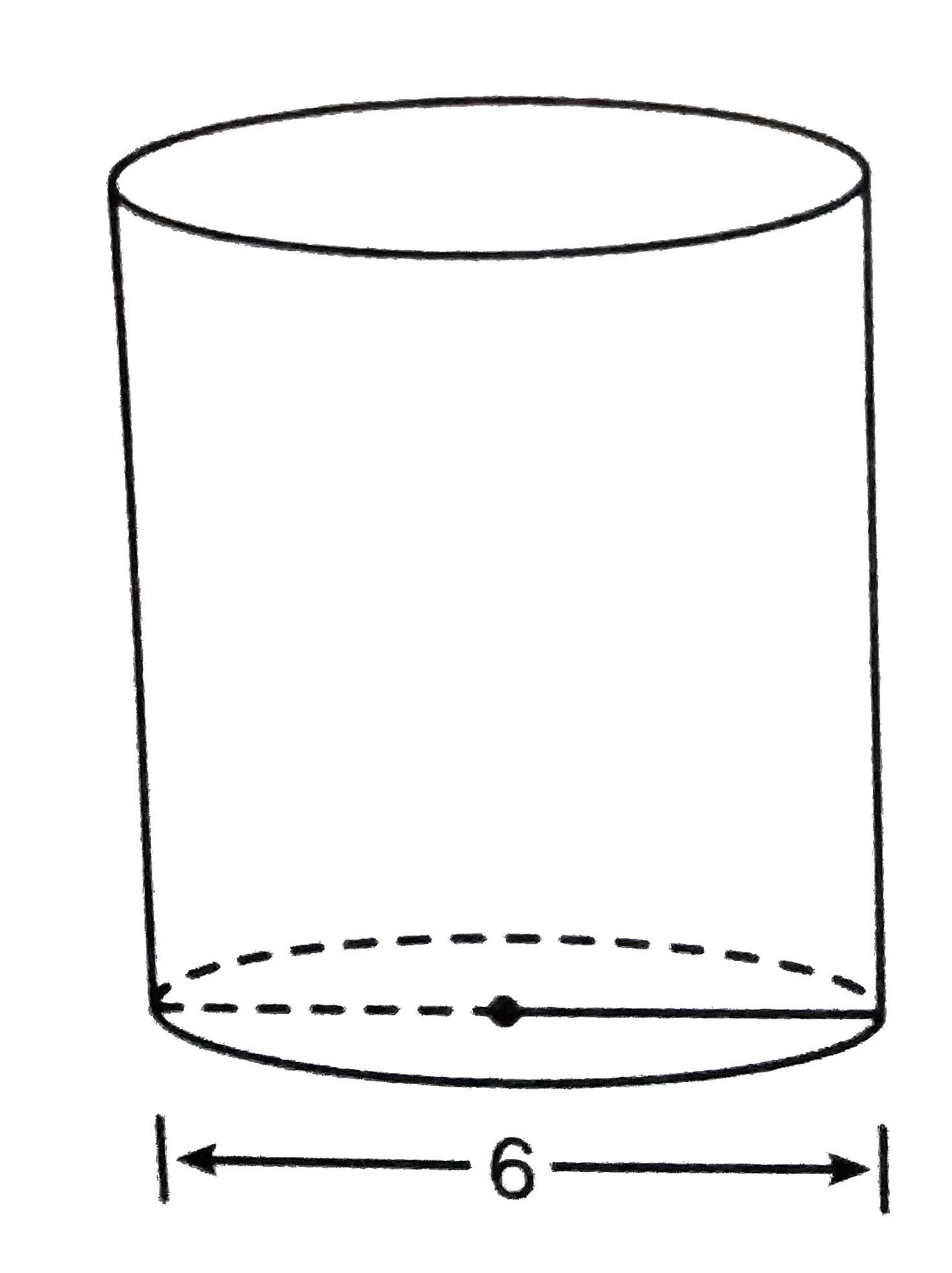
The diameter of the base of a right circular cylinder is 6 and the distance from the centre of a base to a point on the circumference of the other base is 8 what is the height of the cylinder?A2B10C√10D√55If on one helix of DNA the base is cytosine the other helix could have
AadenineBguanineCthymineDuracil
The base of a triangle is 80cm and one of the base angles is 60∘.If the sum of the lenghts of the other two sides is 90cm,then the length of the shortest side is
View SolutionProve that the angle between internal bisector of one base angle and the external bisector of the other base angle of a triangle is equal to one-half of the vertical angle.
View SolutionProve that the angle between internal bisector of one base angle and the external bisector of the other base angle of a triangle is equal to one half of the vertical angle.
View SolutionWhat is the required condition, if the light incident on one face of a prism, does not emerge from the other face?
View SolutionA ray of light is incident on the hypotenuse of a right-angled prism after travelling parallel to the base inside the prism. If μ is the refractive index of the material of the prism, the maximum value of the base angle for which light is totally reflected from the hypotenuse is
View SolutionA ray of light is normally incident on one face of an equilateral glass prism. Answer the following :
(a) What is the angle of incidence on the first face of the prism?
(b) What is the angle of refraction from the first face of the prism ?
(c) What will be the angle of incidence at the second face of the prism ?
(d) Will the light ray suffer minimum deviation by the prism ?
View Solution
