Given P(x)=x4+ax3+bx2+cx+d such that x=0 is the only real root of P'(x)=0. If P(−1)<P(1), then in the interval [−1,1]
P(-1) is the minimum and P(1) is the maximum of P
P(-1) is not minimum but P (1)is the maximum of P
P(-1) is the minimum and P(1) is not the maximum of P
neither P(-1) is the minimum nor P(1) is the maximum of P
The correct Answer is:B
Step by step video & image solution for Given P(x) =x^(4) +ax^(3) +bx^(2) +cx +d such that x=0 is the only real root of P'(x) =0. If P(-1) lt P(1), then in the interval [-1,1] by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - High Level Problems (HLP)
35 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Exersise-3 Part I
21 Videos
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
5 Videos
Similar Questions
Letf(x)=x4+ax3+bx2+cx+d be a polynomial with real coefficients and real roots. If |f(i)|=1where i=√−1, then the value of a +b+c+d is
View SolutionIf the roots of ax3+bx2+cx+d=0 are in G.P then the roots of dx3−cx2+bx−a=0 are in
View SolutionLet P(x)=x2+12x+b and Q(x)=x2+cx+d be two polynomials with real coefficients such that P(x)Q(x)=Q(P(x)) for all real x. Find all the real roots of P(Q(x)) =0.
View SolutionIf P(x)=ax2+bx+c, and Q(x)=−ax2+dx+c,ax≠0 then prove that P(x),Q(x)=0 has atleast two real roots.
View SolutionLet Pn(x)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
View SolutionLet a,b,c∈R with a>0 such that the equation ax2+bcx+b3+c3−4abc=0 has non-real roots.
If P(x)=ax2+bx+candQ(x)=ax2+cx+b, then (a) P(x)>0 for all x∈R and Q(x)<0 for all x∈R. (b) P(x)<0 for all x∈RandQ(x)>0 for all x∈R. (c) neither P(x)>0 for all x∈R nor Q(x)>0 for all x∈R. (d) exactly one of P(x) or Q(x) is positive for all real x.
View SolutionLet Pn(ix)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
View SolutionLet Pn(ix)=1+2x+3x2+............+(n+1)xn be a polynomial such that n is even.The number of real roots of Pn(x)=0 is
View SolutionIn the given figure graph of y=p(x)=x4+ax3+bx2+cx+d is given
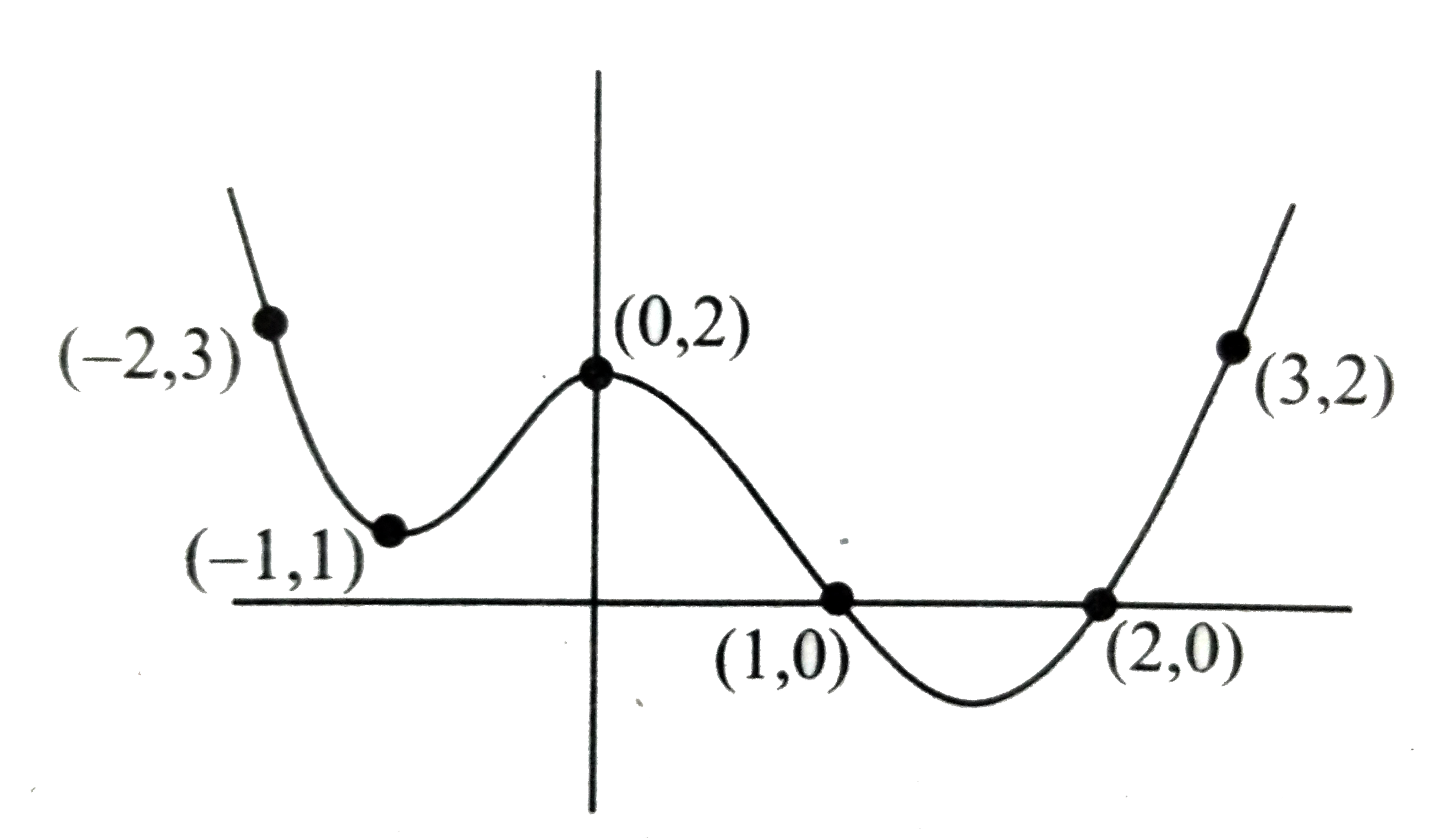
The product of all imaginary roots of p(x)=0 is (a) 1 (b) 2 (c) 13 (d) 14
View SolutionLet f(x)=x3+x+1 and P(x) be a cubic polynomial such that P(0) = -1 and roots of f(0) = 1 ; P(x) = 0 are the squares of the roots of f(x) = 0 . Then find the value of P(4).
View Solution
