When a voltage Vs=200√2sin(100t)V is applied to an ac circuit the current in the circuit is found to be i=2sin[ωt+(π/4)]A. Find the average power consumed in the circuit.
To find the average power consumed in the circuit, we can follow these steps:
Step 1: Identify the given voltage and current equations
The voltage applied to the circuit is given as:
Vs=200√2sin(100t)V
The current in the circuit is given as:
i=2sin(ωt+π4)A
Step 2: Determine the peak voltage and peak current
From the voltage equation, we can identify the peak voltage (V0):
V0=200√2V
From the current equation, we can identify the peak current (I0):
I0=2A
Step 3: Calculate the RMS values of voltage and current
The RMS (Root Mean Square) values are calculated as follows:
Vrms=V0√2=200√2√2=200V
Irms=I0√2=2√2=√2A
Step 4: Determine the phase difference (ϕ)
From the current equation, we see that the phase angle is:
ϕ=π4
Step 5: Calculate the average power consumed in the circuit
The average power P consumed in an AC circuit is given by the formula:
P=Vrms⋅Irms⋅cos(ϕ)
Substituting the values we found:
P=200⋅√2⋅cos(π4)
Since cos(π4)=1√2:
P=200⋅√2⋅1√2=200W
Final Answer
The average power consumed in the circuit is:
200W
The voltage applied to the circuit is given as:
Vs=200√2sin(100t)V
The current in the circuit is given as:
i=2sin(ωt+π4)A
From the voltage equation, we can identify the peak voltage (V0):
V0=200√2V
I0=2A
The RMS (Root Mean Square) values are calculated as follows:
Vrms=V0√2=200√2√2=200V
Irms=I0√2=2√2=√2A
From the current equation, we see that the phase angle is:
ϕ=π4
The average power P consumed in an AC circuit is given by the formula:
P=Vrms⋅Irms⋅cos(ϕ)
Substituting the values we found:
P=200⋅√2⋅cos(π4)
Since cos(π4)=1√2:
P=200⋅√2⋅1√2=200W
The average power consumed in the circuit is:
200W
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE SECTION A4videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - SECTION B15videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - EXAMPLE40videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
Similar Questions
When a voltage vS=200√2sin(ωt+15∘) is applied to an AC circuit the current in the circuit is found to be i=2sin(ωt+π/4) then average power concumed in the circuit is
(A)200 watt , (B)400√2 watt , (C )100√6 watt , (D)200√2 wattView SolutionWhen an alternating emf e=310sin(100πt)V is applied to a series LCR circuit, current flowing through it is i=5sin(100πt+π/3)A.
Calculate the average power consumed by the circuit.View Solution
Knowledge Check
- Question 1 - Select One
An alternating voltage (in volts) given by V=200√2sin(100t) is connected to 1μF capacitor through an ideal ac ammeter in series. The reading of the ammeter and the average power consumed in the circuit shall be
A20 mA, 0B20 mA, 4WC20√2mA,8WD20√2mA,4√2W
Voltage applied to an AC circuit and current flowing in it is given by
V=200√2sin(ωt+π4) and i=−√2cos(ωt+π4)
Then, power consumed in the circuited will beView SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
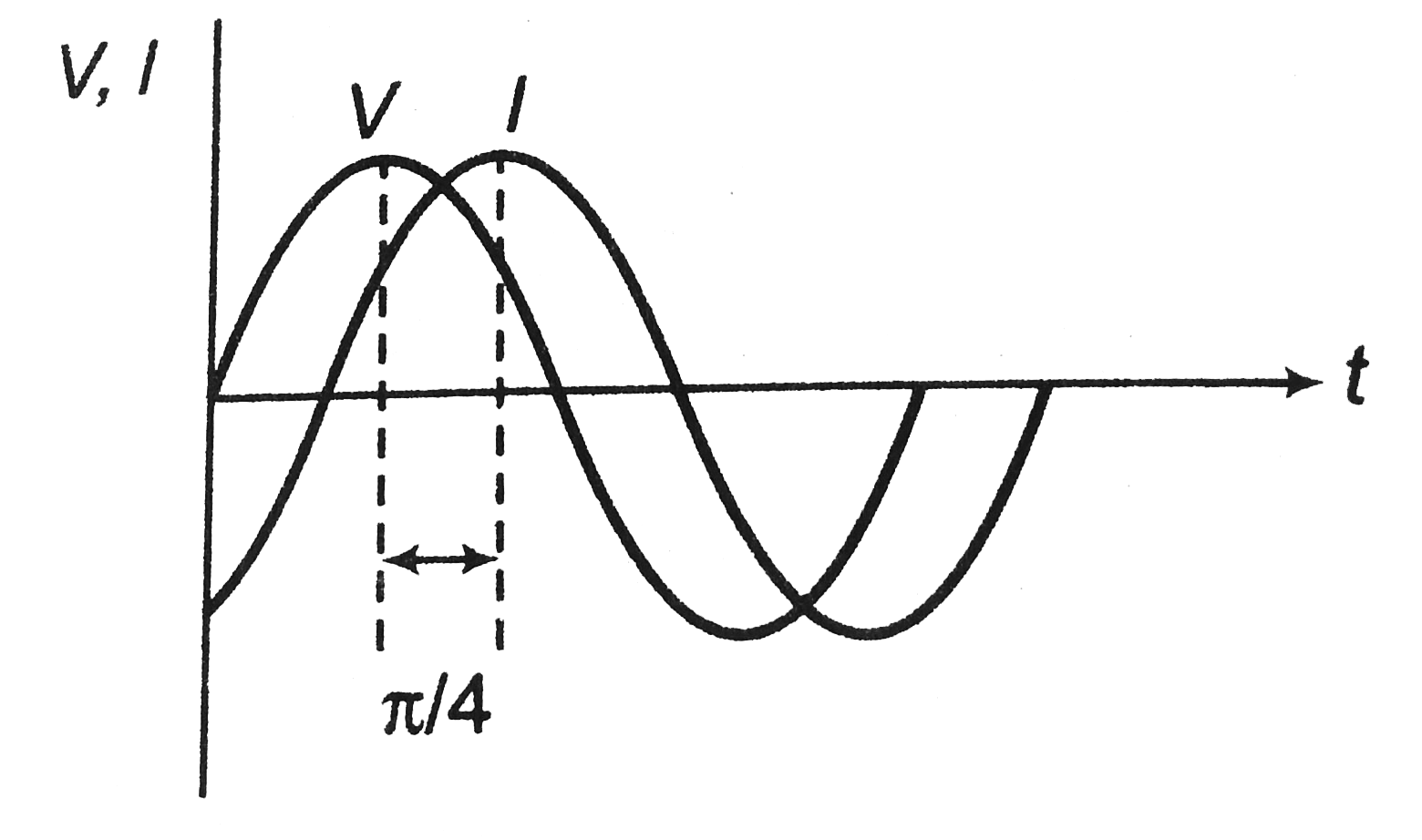 .View Solution
.View SolutionAn Ac voltage V=V0sin100t is applied to the circuit, the phase difference between current and voltage is found to be π4, then
 .View Solution
.View SolutionVoltage input in a circuit is V = 300 sin(ωt) with current = 100 cos(ωt) . Average power loss in the circuit is
View SolutionCurrent in an ac circuit is given by i=2√2sin[(πt+((π)/4)]. Then find the average value of current during time t=0 to t=1 s.
View SolutionCurrent in an ac circuit is given by i=2√2sin[(πt+((π)/4)]. Then find the average value of current during time t=0 to t=1 s.
View SolutionCurrent in an ac circuit is given by I=3sinωt+4cosωt, then
View Solution

