A capactor is connected withan ac source through an ac ammeter (it reads rms value). What will be the reading of the ammeter?
To find the reading of the ammeter when a 10µF capacitor is connected to an AC source given by E=200√2sin(100t)V, we can follow these steps:
Step 1: Identify the peak voltage (V₀)
The given equation for the voltage is in the form E=V₀sin(ωt), where:
- V₀ = 200√2 V
Step 2: Calculate the capacitive reactance (Xc)
The capacitive reactance \(X_c\) is given by the formula:
\(
X_c = \frac{1}{\omega C}
\)
where:
- \(C = 10 \mu F = 10 \times 10^{-6} F\)
- \(\omega = 100 \, \text{rad/s}\) (from the equation)
Substituting the values:
\(
X_c = \frac{1}{100 \times 10 \times 10^{-6}} = \frac{1}{1 \times 10^{-3}} = 1000 \, \Omega
\)
Step 3: Calculate the peak current (I₀)
The peak current \(I₀\) can be calculated using Ohm's law for AC circuits:
\(
I₀ = \frac{V₀}{X_c}
\)
Substituting the values:
\(
I₀ = \frac{200\sqrt{2}}{1000} = \frac{200\sqrt{2}}{1000} = 0.2828 \, A \quad (\text{approximately})
\)
Step 4: Convert peak current to RMS current (Irms)
The RMS current \(I_{rms}\) is related to the peak current by:
\(
I_{rms} = \frac{I₀}{\sqrt{2}}
\)
Substituting the value of \(I₀\):
\(
I_{rms} = \frac{0.2828}{\sqrt{2}} = \frac{0.2828}{1.4142} = 0.2 \, A
\)
Step 5: Convert to milliampere
To express the current in milliamperes:
\(
I_{rms} = 0.2 \, A = 200 \, mA
\)
Final Answer
The reading of the ammeter will be 200 mA.
---
The given equation for the voltage is in the form E=V₀sin(ωt), where:
- V₀ = 200√2 V
The capacitive reactance \(X_c\) is given by the formula:
\(
X_c = \frac{1}{\omega C}
\)
where:
- \(C = 10 \mu F = 10 \times 10^{-6} F\)
- \(\omega = 100 \, \text{rad/s}\) (from the equation)
\(
X_c = \frac{1}{100 \times 10 \times 10^{-6}} = \frac{1}{1 \times 10^{-3}} = 1000 \, \Omega
\)
The peak current \(I₀\) can be calculated using Ohm's law for AC circuits:
\(
I₀ = \frac{V₀}{X_c}
\)
Substituting the values:
\(
I₀ = \frac{200\sqrt{2}}{1000} = \frac{200\sqrt{2}}{1000} = 0.2828 \, A \quad (\text{approximately})
\)
The RMS current \(I_{rms}\) is related to the peak current by:
\(
I_{rms} = \frac{I₀}{\sqrt{2}}
\)
Substituting the value of \(I₀\):
\(
I_{rms} = \frac{0.2828}{\sqrt{2}} = \frac{0.2828}{1.4142} = 0.2 \, A
\)
To express the current in milliamperes:
\(
I_{rms} = 0.2 \, A = 200 \, mA
\)
The reading of the ammeter will be 200 mA.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - EXERCISE SECTION A4videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - SECTION B15videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - EXAMPLE40videos
ALTERNATING CURRENT
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
Similar Questions
A cell of e.m.f. 1.8 V and internal resistance 2 Ω is connected in series with an ammeter of resistance 0.7 Ω and a resistor of 4.5 Ω as shown in Fig.
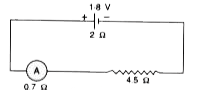
What would be the reading of the ammeter ?View SolutionA capacitor of capacitance 10μF is connected to an AC source and an AC Ammeter. If the source voltage varies as V=50√2sin100t, the reading of the ammeter is
View Solution
Knowledge Check
- Question 1 - Select One
A 5μF capacitor is connected to a 200 V, 100 Hz ac source. The capacitive reactance is
A212ΩB312ΩC318ΩD412Ω - Question 2 - Select One
An alternating voltage (in volts) given by V=200√2sin(100t) is connected to 1μF capacitor through an ideal ac ammeter in series. The reading of the ammeter and the average power consumed in the circuit shall be
A20 mA, 0B20 mA, 4WC20√2mA,8WD20√2mA,4√2W
A 10 muF capacitor, an inductor and a resistor of 100Omega are connected to an alternating source of emf 200sqrt2 sin 100t as shown in the figure. What is the r.m.s current in the circuit and the value of the inductance if the current and the source voltage attain their maxima simultaneously? What is the average power consumed in this case
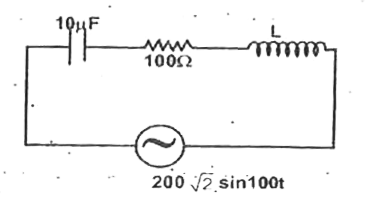 View Solution
View SolutionThe diagram in Fig. shows a cell of e.m.f. ε=2 volt and internal resistance r = 1 ohm connected to an external resistance R = 4 ohm. The ammeter A measures the current in the circuit and the voltmeter V measures the terminal voltage across the cell. What will be the readings of the ammeter and voltmeter when
the key K is closed.
 View Solution
View SolutionThe diagram in Fig. shows a cell of e.m.f. ε=2 volt and internal resistance r = 1 ohm connected to an external resistance R = 4 ohm. The ammeter A measures the current in the circuit and the voltmeter V measures the terminal voltage across the cell. What will be the readings of the ammeter and voltmeter when
the key K is open
 View Solution
View SolutionAn alternating voltage E=200√2sin(100t) is connected to a 1 microfarad capacitor through an AC ammeter. The reading of the ammeter shall be
View SolutionAn alternating voltage E=200√2sin(100t) is connected to a 1 microfarad capacitor through an AC ammeter. The reading of the ammeter shall be
View SolutionA dc ammeter and a hot wire ammeter are connected to a circuit in series. When a direct current is passed through circuit, the dc ammeter shows 6 A. When ac current flows through circuit, the ac ammeter shows 8A. What will be reading of each ammeter if dc and ac current flow simulataneously through the circuit?
View Solution

