A resistor R an inductance L and a capacitor C are all connected in series with an ac supply The resistance of R is 16ohm and for the given frequency the inductive reactance of L is 24 ohm and the capacitive reactance of C is 12ohm If the current in the circuit is 5A find
(a) the potential difference across R,L and C
(b) the impedance of the circuit
(c) the voltage of the ac supply and
(d) the phase angle .
Let's solve the problem step by step.
Given Data:
- Resistance, R=16Ω
- Inductive reactance, XL=24Ω
- Capacitive reactance, XC=12Ω
- Current, I=5A
(a) Potential Difference Across R,L, and C
1. Potential Difference Across Resistor R:
VR=I×R=5A×16Ω=80V
2. Potential Difference Across Inductor L:
VL=I×XL=5A×24Ω=120V
3. Potential Difference Across Capacitor C:
VC=I×XC=5A×12Ω=60V
Summary of Part (a):
- VR=80V
- VL=120V
- VC=60V
(b) Impedance of the Circuit
The impedance Z in a series RLC circuit is given by:
Z=√R2+(XL−XC)2
1. Calculate XL−XC:
XL−XC=24Ω−12Ω=12Ω
2. Substitute into the impedance formula:
Z=√162+122=√256+144=√400=20Ω
Summary of Part (b):
- Impedance Z=20Ω
(c) Voltage of the AC Supply
The voltage of the AC supply V can be calculated using:
V=I×Z
1. Substitute the values:
V=5A×20Ω=100V
Summary of Part (c):
- Voltage of the AC supply V=100V
(d) Phase Angle
The phase angle ϕ can be calculated using:
tanϕ=XL−XCR
1. Substitute the values:
tanϕ=1216=34
2. Calculate ϕ:
ϕ=tan−1(0.75)≈36.86∘
Summary of Part (d):
- Phase angle ϕ≈36.86∘
Final Answers:
- (a) VR=80V, VL=120V, VC=60V
- (b) Z=20Ω
- (c) V=100V
- (d) ϕ≈36.86∘
---
- Resistance, R=16Ω
- Inductive reactance, XL=24Ω
- Capacitive reactance, XC=12Ω
- Current, I=5A
VR=I×R=5A×16Ω=80V
VL=I×XL=5A×24Ω=120V
VC=I×XC=5A×12Ω=60V
- VR=80V
- VL=120V
- VC=60V
Z=√R2+(XL−XC)2
XL−XC=24Ω−12Ω=12Ω
Z=√162+122=√256+144=√400=20Ω
- Impedance Z=20Ω
V=I×Z
V=5A×20Ω=100V
- Voltage of the AC supply V=100V
tanϕ=XL−XCR
tanϕ=1216=34
ϕ=tan−1(0.75)≈36.86∘
- Phase angle ϕ≈36.86∘
- (a) VR=80V, VL=120V, VC=60V
- (b) Z=20Ω
- (c) V=100V
- (d) ϕ≈36.86∘
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - SOLVED EXAMPLES
24 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - PRACTICE EXERCISE 1
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
Similar Questions
A resistor R, an inductor L and a capacitor C are connected in series to an oscillator of frequency n. If the resonant frequency is nr, then the current lags behind voltage, when
View SolutionA resistor R,an inductor L, and a capacitor C are connected in series to an oscillator of freqency υ.if the resonant frequency is υr, then the current lags behind voltage, when:
View Solution
Knowledge Check
Assertion : In series LCR resonance circuit, the impedance is equal to the ohmic resistance.
Reason : At resonance, the inductive reactance exceeds the capacitive reactance.AIf both assertion ans reason are true ans reaason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion istrue but reason is false.DIf both assertion and reason are false.
In a circuit containing R and L , as the frequency of the impressed AC increase, the impedance of the circuit
View SolutionA resistance (R) = 12 Omega, inductance (L) = 2 henry and capacitive reactance C = 5 mF are connected in series to an ac generator
View SolutionWith increase in frequency of an AC supply, the inductive reactance:
View SolutionFigure below shows a capacitor C, an inductor L and a resistor R, connected in series to an a.c. supply of 220 V.
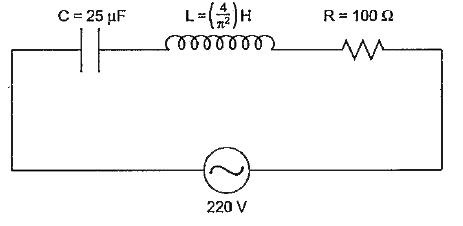
The resonant frequency of the given RLC circuit.
View SolutionIf resistance R =100 Omega, inductance L = 12mH and capacitance C=15muF are connected in series to an AC sources, then at resonance the impedance of circuit is
View SolutionIf resistance R =10Ω, inductance L = 2 mH and capacitance C=5μF are connected in series to an AC source of frequency 50 Hz, then at resonance the impedance of circuit is
View SolutionAn AC voltage is applied to a resistance R and an inductance L in series. If R and the inductive reactance are both equal to 3Ω, the phase difference between the applied voltage and the current in the circuit is
View Solution