A conductor of capacitance 10μF connected to other conductor of capacitance 40μF having equal charges 100μC initially. Find out final voltage and heat loss during the process?
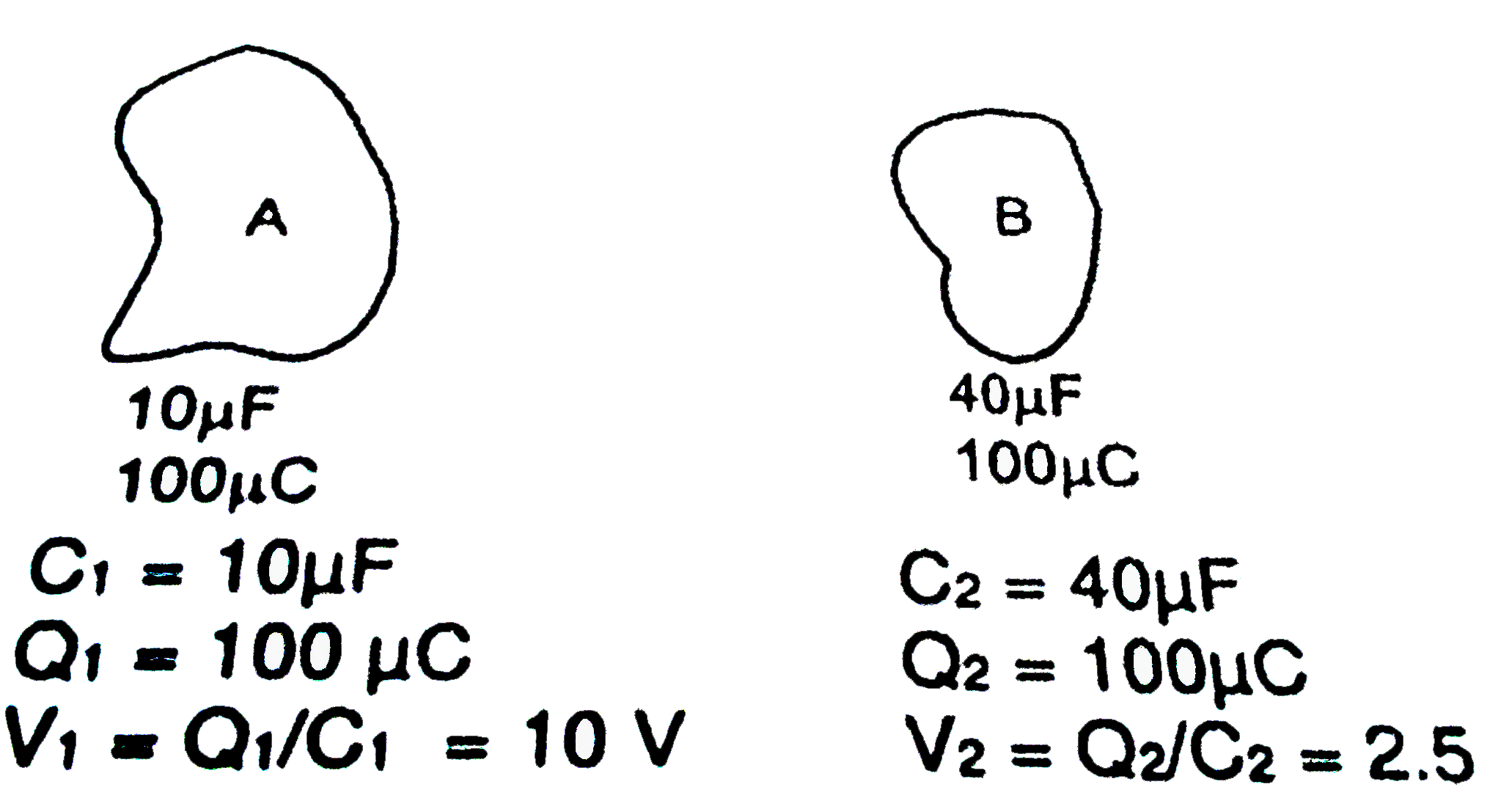
10μF 40μF
100μC 100μC
C1=10μF C2=40μF
Q1=100μC C2=100μC
V1=Q1/C1=10V V2=Q2/C2=2.5
Final voltage (V) =C1V1+C(2)V2(C1+C2)=Q1+Q2C1+C2=200μC50μF=4V
Heat loss during the process =12[C1C21+C2V22]−12V2(C1+C2)
=12[Q1V1+Q2V2]−12V2(C1+C2)=12×100μ[12.5]−12×16(50)μ=225μJ
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 179videos
CAPACITANCE
- BOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - Exercise - 274videos
CAPACITANCE
- BOOK - RESONANCE ENGLISHCHAPTER - CAPACITANCEEXERCISE - High Level Problems16videos
CAPACITANCE
- BOOK - RESONANCE ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - Advanved level problems17videos
ATOMIC PHYSICS
- BOOK - RESONANCE ENGLISHCHAPTER - COMMUNICATION SYSTEMSEXERCISE - Exercise 313videos
COMMUNICATION SYSTEMS
Similar Questions
An inductor of inductance 2.0mH s connected across a charged capacitor of capacitance 5.0μF and the resulting LC circuit is set oscillating at its natural frequency. Let Q denote the instantaneous charge on the capacitor and I the current in the circuit. It is found that the maximum value of charge Q is 200μC.
a. When Q=100μC, what is the value of ∣∣∣dIdt∣∣∣?
b. When Q=200μC, what is the value of I?
c. Find the maximum value of I.
d. When I is equal to one-half its maximum value, what is the value of |Q|?View SolutionThe charge on the condenser of capacitance 2μF in the following circuit will be -
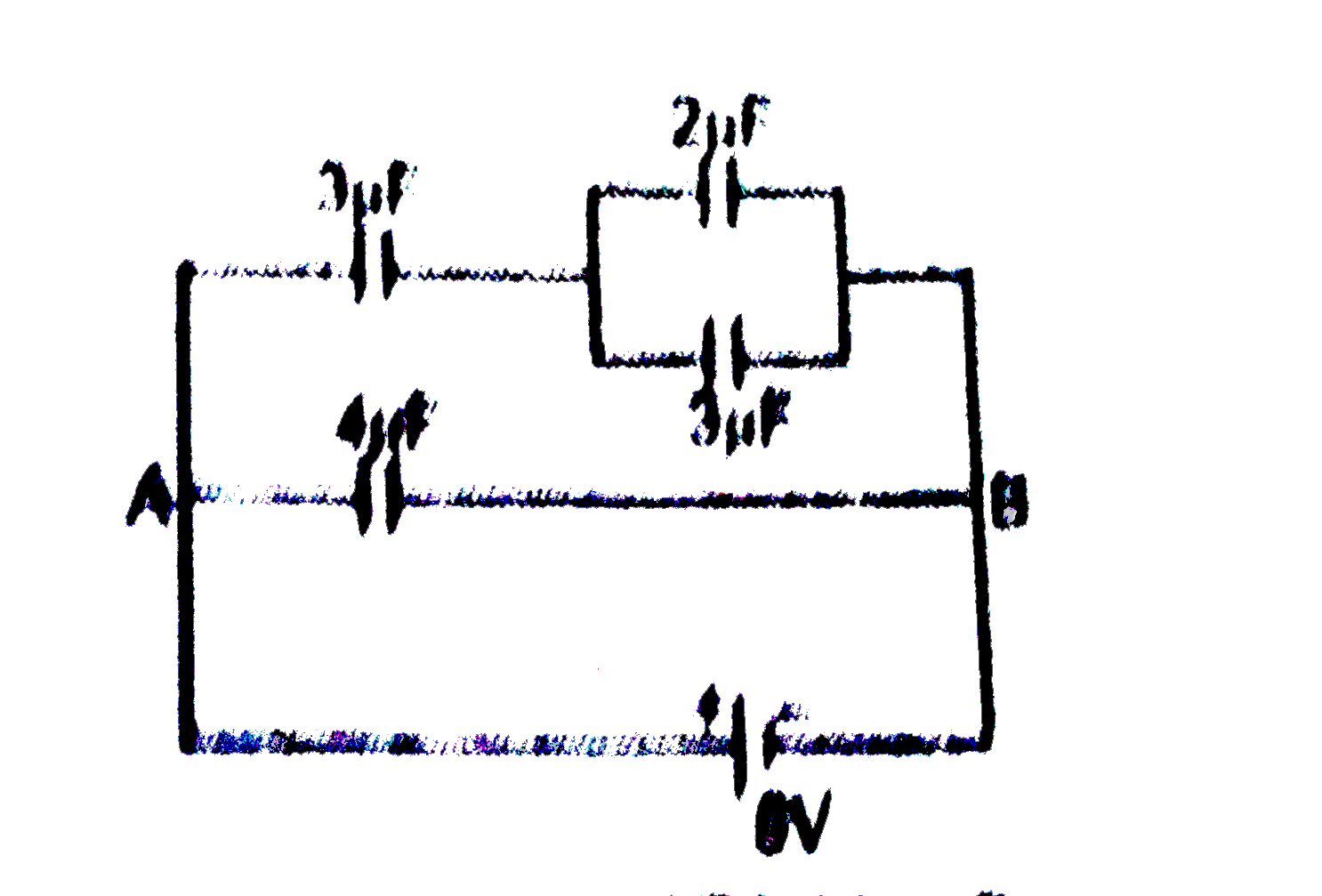 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A 5μF capacitor is connected to a 200 V, 100 Hz ac source. The capacitive reactance is
A212ΩB312ΩC318ΩD412Ω
An inductor of inductance 20 mH is connected across a charged capacitor of capacitance 5 μF & resulting L-C circuit is set oscillating at its natural frequency . The maximum charge q is 200 μ C on the capacitor . Find the potential difference across the inductor when the charge is 100 μC .
View SolutionA capacitor of capacitance C0 is charged to potential V0. Now it is connected to another uncharged capacitor of capacitance C02. Calculate the heat loss in this process.
View SolutionA capacitor of capacitance 6 μF is connected with an emf sourface 3 V. Electrostaci energy stored in the capacitor is
View SolutionA capacitor A of capacitance 4μF is charged to 30V and another capacitor B of capacitance 2μF is charged to 15V. Now, the positive plate of A is connected to the negative plate of B and negative plate of A to the positive plate of B. find the final charge of each capacitor and loss of electrostatic energy in the process.
View SolutionA capacitor of capacitance 10(μ)F is connected to a battery of emf 2V.It is found that it takes 50 ms for the charge on the capacitor to bacome 12.6(μ)C.find the resistance of the circuit.
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :View Solution

