An inductor of inductance 2.0mH s connected across a charged capacitor of capacitance 5.0μF and the resulting LC circuit is set oscillating at its natural frequency. Let Q denote the instantaneous charge on the capacitor and I the current in the circuit. It is found that the maximum value of charge Q is 200μC.
a. When Q=100μC, what is the value of ∣∣∣dIdt∣∣∣?
b. When Q=200μC, what is the value of I?
c. Find the maximum value of I.
d. When I is equal to one-half its maximum value, what is the value of |Q|?
When Q=100μC, what is the value of \dI/dt\?
When Q=200μC what is the value of I?
Find the maximum value of I.
When I is equal to one-half of its maximum value, what is the value of |Q|?
This is a problem L−C oscillations.
Charge stored in the capacitor oscillates simple harmonically as
Q=Q0sin(ωt±ϕ)
Here Q0=maximum value of Q=200μC=2×10−4C
ω=1√LC=1√(2×10−3)(5.0×10−6)=104s−1
Let at t=0,Q=Q0 then
Q(t)=Q0cosωt ........i
I(t)=dQdt=−Q0ωsinωt and ........ii
dI(t)dt=−Q0ω2cosωt ............iii
a. Q=100μC
or Q02 at cosωt=12
or ωt=π3
At cosωt=12, from eqn iii:
∣∣∣dIdt∣∣∣=(2.0×10−4C)(104s−1)2(12)
∣∣∣dIdt∣∣∣=104A/s
b. Q=200μC or Q0 when cosωt=1, i.e. cosωt=0,2π........
At the time I(t)=−Q0ωsinωt
or I(t)=0(sin02=sin2π=0)
c. I(t)=−Q0ωsinωt
∴ Maximum value of I is Q0ω
Imax=Q0ω=(2.0×10−4)(104)
Imax=2.0A
d. From energy conservation
12LI2max=12LI2+12Q2C
or Q=√LC(I2max−I2)
I=Imax2=1.0A
∴Q=√(2.0×10−3)(5.0×10−−6)(22−12)
Q=√3×10−4C
or Q=1.732×10−4C
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 52videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 63videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Example Type 34videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEY ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEY ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
An inductor of inductance 20 mH is connected across a charged capacitor of capacitance 5 μF & resulting L-C circuit is set oscillating at its natural frequency . The maximum charge q is 200 μ C on the capacitor . Find the potential difference across the inductor when the charge is 100 μC .
View SolutionAn inductor of inductance 2 mH is connected across a charged capacitor of 5 μ F . Let q denote the instaneous charge on the capacitor and i the current in the circuit . Maximum value of charge is Q = 200 μ C.
(a) When Q = 100 μ C what is the value of /di/dt / ?
(b) When Q = 200 μ C what is the value of i ?View SolutionThe charge on the condenser of capacitance 2μF in the following circuit will be -
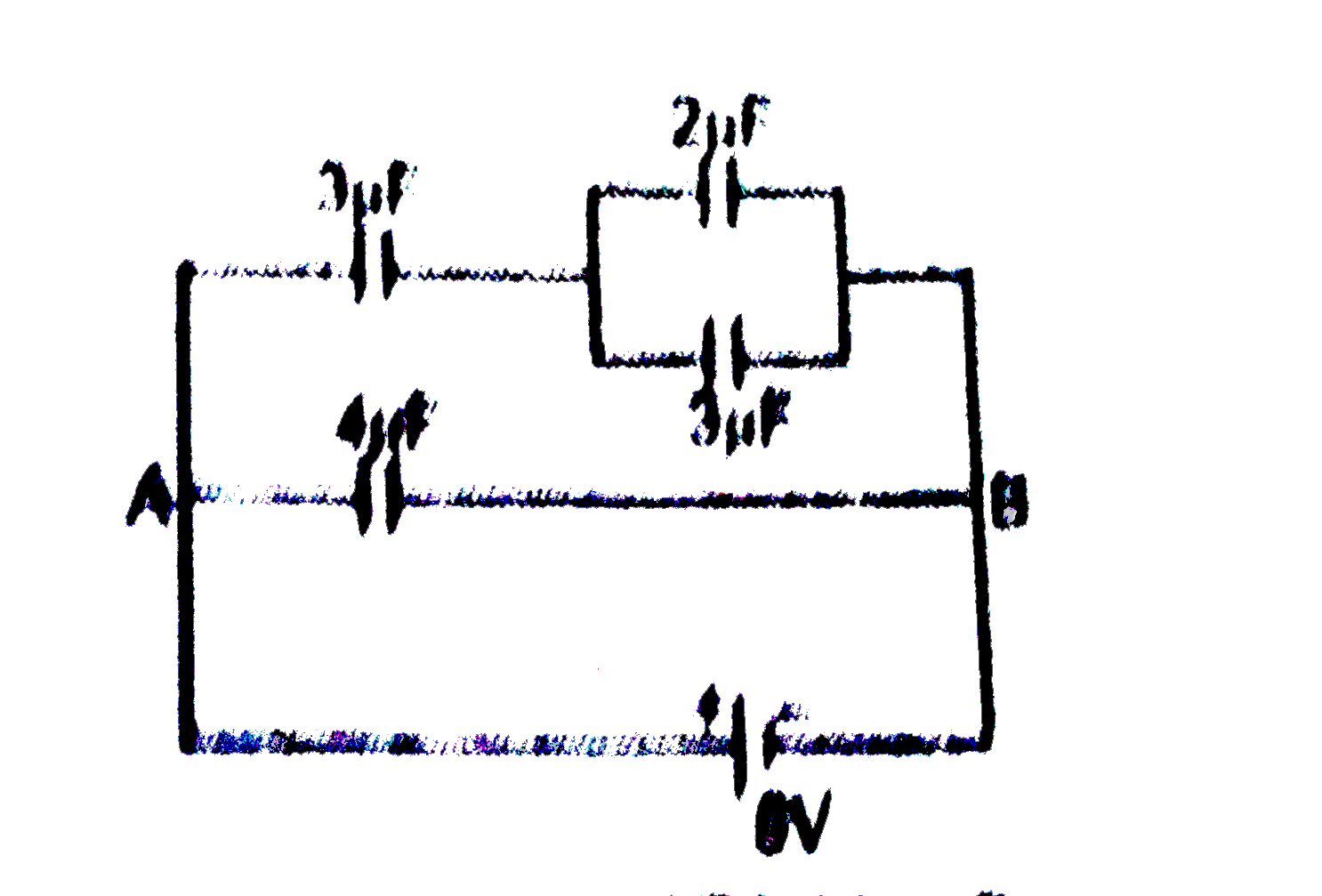 View Solution
View SolutionThe charge on 4μFcapacitor in the given circuit is (inμC)
 View Solution
View SolutionThe charge in the 2μF capacitor at steady state is
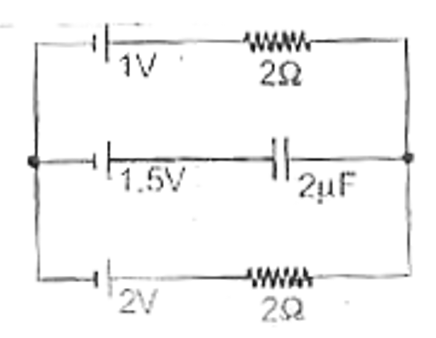 View Solution
View SolutionIn the circuit shown , charge on the 5μF capacitor is :
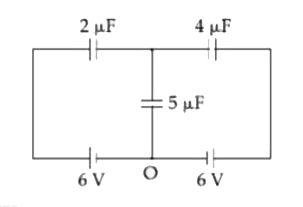 View Solution
View SolutionIn the given circuit, the charge on 4μF capacitor will be :
 View Solution
View SolutionA capacitor of capacitance 2μF is connected in the tank circuit of an oscillator oscillating with a frequency of 1 kHz. If the current flowing in the circuit is 2mA, the voltage across the capacitor will be
View SolutionIn the given circuit, the charge on 4μF capacitor will be :
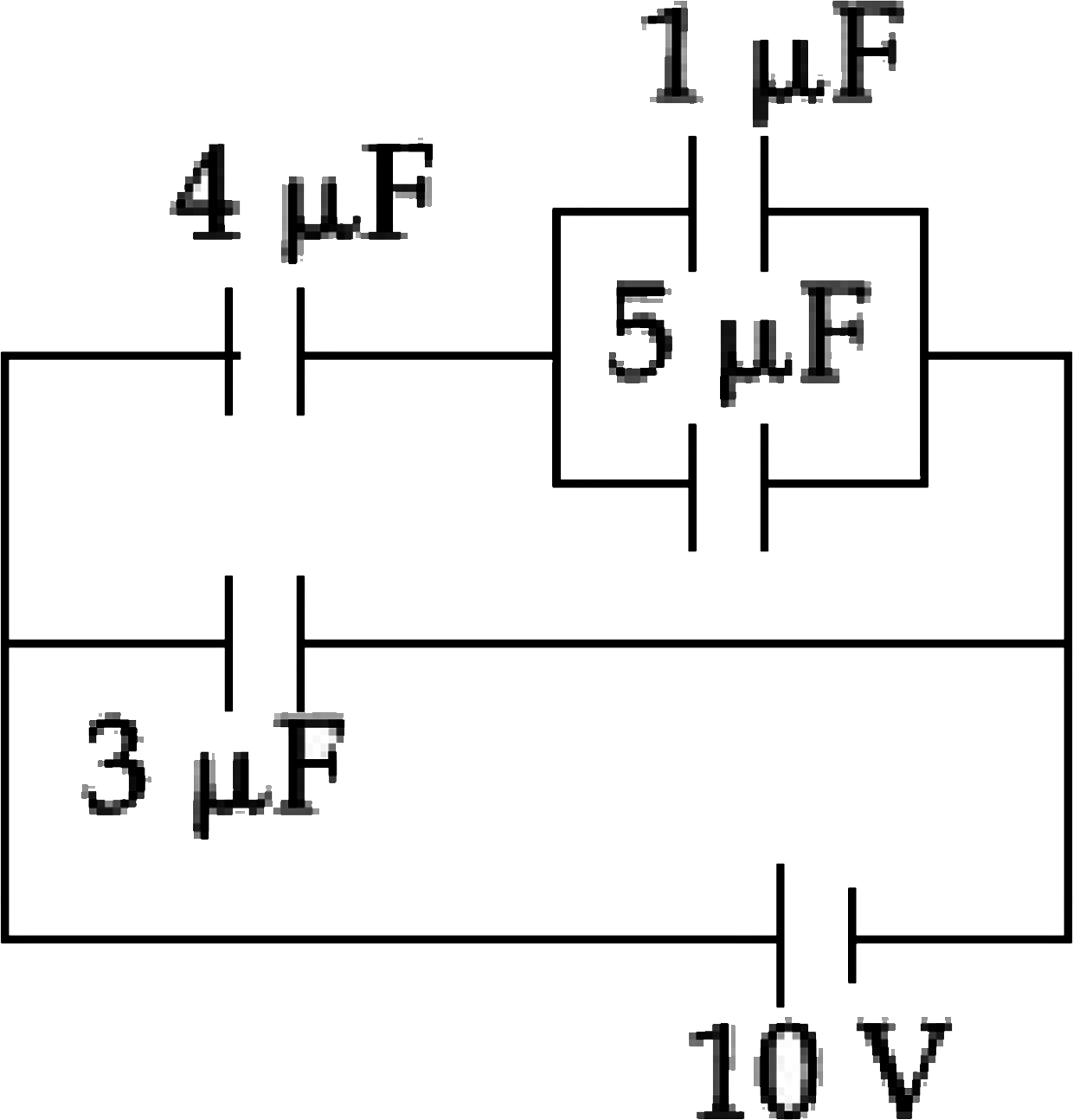 .View Solution
.View SolutionA capacitor of capacitance 1μF is charged to potential 2 V and is connected to an inductor of 1 mH. At an instant when potential difference across. The capacitor is 1 V, the current in the circuit is 10−2√10x3 ampere. Find out the value of x.
View Solution

