Rate of increment of energy in an inductor with time in series RL circuit getting charged with battery of EMF Eis best represented by:
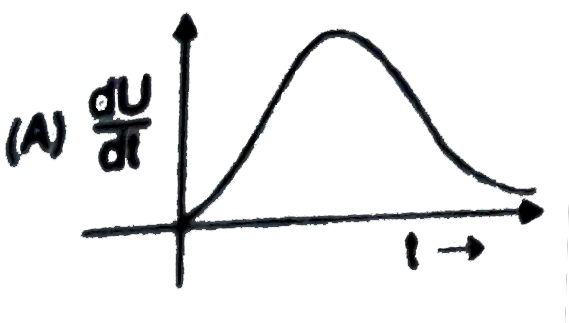


The correct Answer is:A
To solve the problem of finding the rate of increment of energy in an inductor with time in a series RL circuit being charged by a battery of EMF E, we can follow these steps:
Step 1: Understand the Energy in an Inductor
The energy stored in an inductor U is given by the formula:
U=12LI2
where L is the inductance and I is the current through the inductor.
Step 2: Differentiate the Energy with Respect to Time
To find the rate of change of energy with respect to time, we differentiate U:
dUdt=ddt(12LI2)
Since L is a constant, we can take it out of the differentiation:
dUdt=L⋅I⋅dIdt
This is our Equation (1).
Step 3: Determine the Current in the RL Circuit
The current I in an RL circuit at any time t can be expressed as:
I=I0(1−e−tτ)
where I0 is the maximum current and τ=LR is the time constant of the circuit.
Step 4: Differentiate the Current with Respect to Time
Now, we differentiate I with respect to time t:
dIdt=I0⋅ddt(1−e−tτ)
The derivative of e−tτ is:
−1τe−tτ
Thus,
dIdt=I0⋅(0+1τe−tτ)=I0τe−tτ
This is our Equation (2).
Step 5: Substitute dIdt into dUdt
Now we substitute Equation (2) into Equation (1):
dUdt=L⋅I⋅dIdt=L⋅I0(1−e−tτ)⋅I0τe−tτ
This simplifies to:
dUdt=LI20τ(1−e−tτ)e−tτ
Step 6: Analyze the Behavior at t=0 and t→∞
- At t=0:
dUdt=LI20τ⋅0⋅1=0
- As t→∞:
dUdt=LI20τ⋅1⋅0=0
Conclusion
The rate of increment of energy in the inductor starts from zero, increases to a maximum, and then returns to zero as the current stabilizes. Therefore, the best representation of the rate of increment of energy in the inductor over time is a function that starts and ends at zero.
Final Answer
The correct option is A.
The energy stored in an inductor U is given by the formula:
U=12LI2
where L is the inductance and I is the current through the inductor.
To find the rate of change of energy with respect to time, we differentiate U:
dUdt=ddt(12LI2)
Since L is a constant, we can take it out of the differentiation:
dUdt=L⋅I⋅dIdt
This is our Equation (1).
The current I in an RL circuit at any time t can be expressed as:
I=I0(1−e−tτ)
where I0 is the maximum current and τ=LR is the time constant of the circuit.
Now, we differentiate I with respect to time t:
dIdt=I0⋅ddt(1−e−tτ)
The derivative of e−tτ is:
−1τe−tτ
Thus,
dIdt=I0⋅(0+1τe−tτ)=I0τe−tτ
This is our Equation (2).
Now we substitute Equation (2) into Equation (1):
dUdt=L⋅I⋅dIdt=L⋅I0(1−e−tτ)⋅I0τe−tτ
This simplifies to:
dUdt=LI20τ(1−e−tτ)e−tτ
- At t=0:
dUdt=LI20τ⋅0⋅1=0
- As t→∞:
dUdt=LI20τ⋅1⋅0=0
The rate of increment of energy in the inductor starts from zero, increases to a maximum, and then returns to zero as the current stabilizes. Therefore, the best representation of the rate of increment of energy in the inductor over time is a function that starts and ends at zero.
The correct option is A.
Similar Questions
When a battery is connected across a series combination of self inductance L and resistance R , the variation in the current i with time t is best represented by
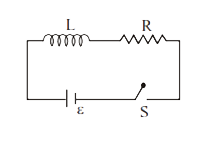
View SolutionAs shown in the figure, a battery of emf is connected to an inductor L and resistance R in series. The switch is closed at . The total charge that flows from the battery, between t=te and t=2te (te is the time constant of the circuit) is:
 View Solution
View SolutionA constant current exists in an inductor coil connected to a battery. The coil is short circuited and the battery is removed. Show that the charge flown through the coil after the short circuiting is the same as that which flows in one time constant before the short circuiting.
View SolutionIn an LR circuit connected to a battery, the rate at which energy is stored in the inductor is plotted against time during the growth of current in the circuit. Which of the following best represents the resulting curve?
View SolutionConsider the RL circuit in Fig. When the switch is closed in position 1 and opens in position 2, electrical work must be performed on the inductor and on the resistor. The energy stored in the inductor is for the resistor energy appears as heat.
a. What is the ratio of PL/PR of the rate at which energy is stored in the inductor to the rate at which energy is dissipated in the resistor?
b. Express the ratio PL/PR as a function of time.
c. If the time constant of circuit is t, what is the time at which PL=PR?View Solution As shown in the figur a battery of emf ∈ is conneced to an inductor L and resistance R in series . The swith is closed at t =0 . The total charge that flows form the battery between t 0 and t=tc (tc is the time constant of the circuit )is : View Solution
As shown in the figur a battery of emf ∈ is conneced to an inductor L and resistance R in series . The swith is closed at t =0 . The total charge that flows form the battery between t 0 and t=tc (tc is the time constant of the circuit )is : View SolutionAs shown in the figure, a battery of emf ε is connected to an inductor L and resistance R in series. The switch is closed at t=0 . The total charge that flows from the battery, between t=te and t=2te (te is the time constant of the circuit) is:
 View Solution
View SolutionAn inductor (L=20mH), a resistor (R=100Ω) and a battery (ε=10V) are connected in series. After along time the circuit is short- circuited and then the battery is disconnected. Find the current in the circuit 1ms after short- circuiting.
View SolutionA 1.5μF capacitor is charged to 20 V. The charging battery is then disconnected , and a 15 mH coil is connected in series with the capacitor so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking the instant at which inductor is connected to the capacitor as t=0.
View SolutionA 1.5μf capacitor is charged to 20 V. The charging battery is then disconnected and a 15 mH coil is connected in series with the capacitance so that LC oscillations occur. Write the equation for variation of charge on capacitor and current in the inductor with time taking at the instant at which inductor is connected to the capacitor at t = 0
View Solution

