The capacitor for capacitance C can be charged ( with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.

After the capacitor gets fully charged S1 is opened and S2 is closed so that the inductor is connected in series with the capacitor. Then,
A. at t=0, energy stored in the circuit is purely in the form of magnetic energy
B. at any time t<0, current in the circuit is in the same direction.
C. at t>0, there is no exchange of energy between the inductor and capacitor
D. at any time t>0, instananeous current in the circuit will have maximum value V√CL, where C is the capacitance and L is the inductance.
The correct Answer is:D
Step by step video & image solution for The capacitor for capacitance C can be charged ( with the help of a resistance R) by a voltage source V, by closing switch S_(1) while keeping switch S_(2) open. The capacitor can be connected in series with an inductor 'L' by closing switch S_(2) and opening S_(1). After the capacitor gets fully charged S_(1) is opened and S_(2) is closed so that the inductor is connected in series with the capacitor. Then, by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The capacitor of capacitance C can be charged (with the help of a resistance R ) by a voltage source V, by closing switch S1 while keeping switch S2 open. The capacitor can be connected in series with an inductor 'L' by closing switch S2 and opening S1.

Initially, the capacitor was uncharged. Now , switch S1 is closed and S2 is kept open. if time constant of this circuit is τ, then
View SolutionThe capacitor of capacitance C can be charged (with the help of a resistance R) by a voltage source V, by closing switch S1 while keeping switch S2 open.The capacitor can be connected in series with an series with an inductor L by closing switch S2 and opening S1.
Initially the capacitor was uncharged.Now switch S1 is closed and S2 is kept open.If time constant of this circuit is τ, then

View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
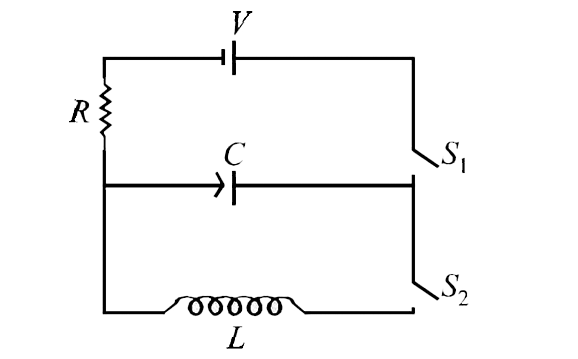
When the capacitor gets charged compleely, (=(S1) is opened and (S2) is closed, Then,
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
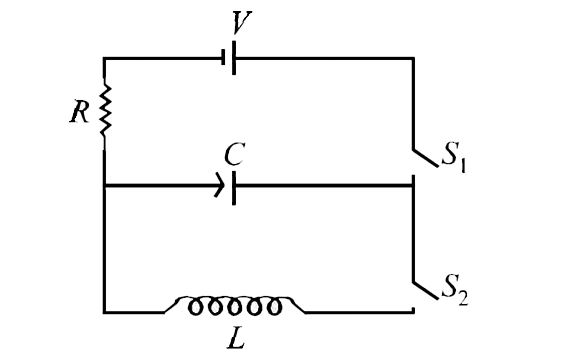
At the start, the capicitor was uncharged. when switch (S1) is closed and (S2) is kept open, the time constant of this circuit is τ. which of the following is correct
View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then

View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then

View SolutionTwo capacitors A and B are connected in series with a battery as shown in the figure. When the switch S is closed and the two capacitors get charged fully, then

View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).
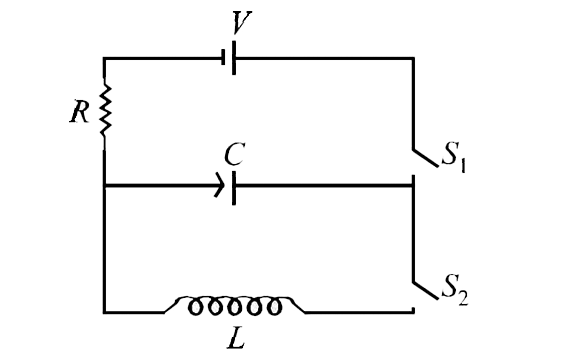
Given taht the total charge stored in the LC circuit is (Q0). for Tge0, the charge on the capacitor is
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).

Given taht the total charge stored in the LC circuit is (Q0). for T≥0 the charge on the capacitor is
View SolutionIn the given circuit the capacitor (C) may be charged through resistance R by a battery V by closing switch (S1). Also when (S1) is opend and (S2) is closed the capacitor is connected in series with inductor (L).

Given taht the total charge stored in the LC circuit is (Q0). for Tge0, the charge on the capacitor is
View Solution
