Determine and draw the graph of electric field due to infinitely large non-conducting sheet of thickness t and uniform volume charge density as a function of distance x from its symmetry plane.
(a) (b)
To determine the electric field due to an infinitely large non-conducting sheet of thickness t and uniform volume charge density ρ, we will analyze the electric field in two regions:
1. When x<t2
2. When x≥t2
Step 1: Understanding the Geometry
- We have an infinitely large non-conducting sheet with thickness t and uniform volume charge density ρ.
- The symmetry plane is at the center of the sheet, which divides it into two halves.
Step 2: Analyze the Electric Field for x<t2
- For points within the thickness of the sheet (i.e., x<t2), we consider a small element of thickness dx at a distance x from the symmetry plane.
- The electric field E produced by this element is directed perpendicular to the sheet.
Step 3: Calculate the Electric Flux
- The electric flux Φ through the area A is given by:
Φ=E⋅A+E⋅A=2EA
- According to Gauss's law, the electric flux is also equal to the charge enclosed divided by ϵ0:
Φ=Qencϵ0
Step 4: Determine Charge Enclosed
- The charge enclosed Qenc can be calculated as:
Qenc=ρ⋅Volume=ρ⋅(2x⋅A)
- Therefore,
Qenc=2ρxA
Step 5: Equate the Two Expressions for Flux
- Setting the two expressions for electric flux equal gives:
2EA=2ρxAϵ0
- Canceling A from both sides, we find:
E=ρxϵ0
- This shows that the electric field E is proportional to x for x<t2.
Step 6: Analyze the Electric Field for x≥t2
- For points outside the sheet (i.e., x≥t2), the entire thickness of the sheet contributes to the electric field.
- The total charge enclosed when x≥t2 is:
Qenc=ρ⋅(t⋅A)
Step 7: Calculate the Electric Flux for Outside the Sheet
- The electric flux is again given by:
2EA=ρtAϵ0
- Canceling A gives:
E=ρt2ϵ0
- This indicates that the electric field E is constant for x≥t2.
Step 8: Graphing the Electric Field
- Now we can plot the graph of electric field E versus distance x:
- For x<t2, E increases linearly with x.
- For x≥t2, E remains constant.
Final Graph:
- The graph will show a linear increase in E from the origin until x=t2, and then a horizontal line representing the constant electric field for x≥t2.
2. When x≥t2
- We have an infinitely large non-conducting sheet with thickness t and uniform volume charge density ρ.
- The symmetry plane is at the center of the sheet, which divides it into two halves.
- For points within the thickness of the sheet (i.e., x<t2), we consider a small element of thickness dx at a distance x from the symmetry plane.
- The electric field E produced by this element is directed perpendicular to the sheet.
- The electric flux Φ through the area A is given by:
Φ=E⋅A+E⋅A=2EA
- According to Gauss's law, the electric flux is also equal to the charge enclosed divided by ϵ0:
Φ=Qencϵ0
- The charge enclosed Qenc can be calculated as:
Qenc=ρ⋅Volume=ρ⋅(2x⋅A)
- Therefore,
Qenc=2ρxA
- Setting the two expressions for electric flux equal gives:
2EA=2ρxAϵ0
- Canceling A from both sides, we find:
E=ρxϵ0
- This shows that the electric field E is proportional to x for x<t2.
- For points outside the sheet (i.e., x≥t2), the entire thickness of the sheet contributes to the electric field.
- The total charge enclosed when x≥t2 is:
Qenc=ρ⋅(t⋅A)
- The electric flux is again given by:
2EA=ρtAϵ0
- Canceling A gives:
E=ρt2ϵ0
- This indicates that the electric field E is constant for x≥t2.
- Now we can plot the graph of electric field E versus distance x:
- For x<t2, E increases linearly with x.
- For x≥t2, E remains constant.
- The graph will show a linear increase in E from the origin until x=t2, and then a horizontal line representing the constant electric field for x≥t2.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Electric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionFind the electric field caused by a disc of radius a with a uniform surfce charge density σ (charge per unit area) at a point along the axis of the disc a distance x from its centre.
View SolutionFind out electric field intensity due to uniformly charged solid non-conducting sphere of volume charge density ρ and radius R at following points :
(i) At a distance r from surface of sphere (inside)
(ii) At a distance r from the surface of sphere (outside)
View SolutionA solid non conducting sphere has charge density pCm−3 Electric field at distance x from its centre is ______ [x<R]
View SolutionTwo infinite parallel,non- conducting sheets carry equal positive charge density σ ,One is placed in the yz plane other at distance x=a Take potential V=0 at x=0 then
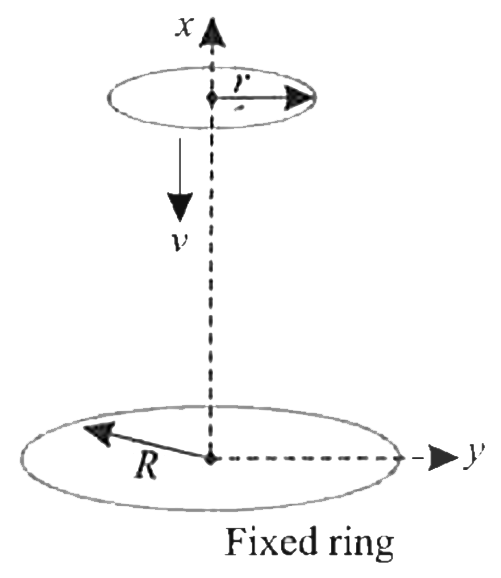
View SolutionA ring of radius R is placed in the plane its centre at origin and its axis along the x-asis and having uniformly distributed positive charge. A ring of radius r(<<R) and coaxial with the larger ring is moving along the axis with constant velcity , then the variation of electrical flux (ϕ) passing through the smaller ring with position will be best represent by :
View SolutionA nonconducting sheet of large surface area and thickness d contains uniform charge distribution of density ρ. Find the electric field at a point P inside the plate, at a distance x from the central plane.
View SolutionA solid non-conduction cylinder of radius R is charge such that volume charge density is proporation to r where r is distance from axis. The electric field E at a distance r(r<R) well depend on r as.
View SolutionThe potential in the electric field varies as V=−ax2+b with respect to x - coordinate, where a and b are constants. Find the charge density ρ(x) in a space.
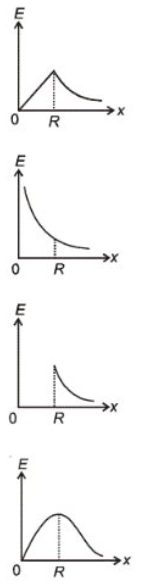
View SolutionA non-conducting solid sphere of radius R, has a uniform charge density. The graph representing variation of magnitude of electric field (E) as a function of distance (x) from the centre of the sphere is
View Solution
