A charged ball of mass 5.88×10−4 kg is suspended from two silk strings of equal lengths so that the strings are inclined at 60∘ with each other. Another ball carrying a charge which is equal in magnitude but opposite in sign of the first one is placed vertically below the first one at a distance of 4.2×10−2m. Due to this, the tension in the strings is doubled. Determine the charge on the ball and the tension in the strings after electrostatic interaction. (g=9.8m/s2)
The correct Answer is:3.36×10−8C,6.65×10−3N
To solve the problem step by step, we will analyze the forces acting on the charged ball and how they change when the second ball is introduced.
Step 1: Analyze the initial equilibrium of the charged ball
- The charged ball of mass m=5.88×10−4kg is suspended by two strings making an angle of 60∘ with each other.
- The angle θ of each string with the vertical is 30∘ (since the strings are inclined at 60∘).
- The weight of the ball is given by mg, where g=9.8m/s2.
Equation for vertical forces:
2Tcos(30∘)=mg
Substituting cos(30∘)=√32:
2T(√32)=mg
T√3=mg
T=mg√3
Step 2: Calculate the initial tension T
Substituting the values:
T=(5.88×10−4kg)(9.8m/s2)√3
Calculating:
T=5.76×10−31.732≈3.32×10−3N
Step 3: Analyze the situation after the second ball is introduced
When the second ball (with charge −q) is placed below the first ball, the tension in the strings doubles:
T′=2T
The new tension is 2T.
Step 4: Write the new equilibrium equation
The new equilibrium condition considering the electrostatic force Fe between the two charges is:
4Tcos(30∘)=mg+Fe
Substituting Fe=14πϵ0q2r2 where r=4.2×10−2m:
4T(√32)=mg+14πϵ0q2(4.2×10−2)2
This simplifies to:
2T√3=mg+14πϵ0q2(4.2×10−2)2
Step 5: Substitute T and simplify
From the previous steps, we know:
2T=2(mg√3)
Substituting this into the equation:
2(mg√3)√3=mg+14πϵ0q2(4.2×10−2)2
This simplifies to:
2mg=mg+14πϵ0q2(4.2×10−2)2
mg=14πϵ0q2(4.2×10−2)2
Step 6: Solve for q2
Rearranging gives:
q2=mg⋅(4.2×10−2)2⋅4πϵ0
Substituting ϵ0=8.85×10−12C2/N m2:
q2=(5.88×10−4⋅9.8)⋅(4.2×10−2)2⋅4π(8.85×10−12)
Step 7: Calculate q
Calculating q2:
q2=(5.76×10−3)⋅(1.764×10−3)⋅(1.112×10−10)
q2≈1.1×10−15
Thus,
q≈√1.1×10−15≈3.3×10−8C
Final Answers
- The charge on the ball is approximately q≈3.3×10−8C.
- The new tension in the strings is T′=2T≈6.64×10−3N.
- The charged ball of mass m=5.88×10−4kg is suspended by two strings making an angle of 60∘ with each other.
- The angle θ of each string with the vertical is 30∘ (since the strings are inclined at 60∘).
- The weight of the ball is given by mg, where g=9.8m/s2.
2Tcos(30∘)=mg
Substituting cos(30∘)=√32:
2T(√32)=mg
T√3=mg
T=mg√3
Substituting the values:
T=(5.88×10−4kg)(9.8m/s2)√3
Calculating:
T=5.76×10−31.732≈3.32×10−3N
When the second ball (with charge −q) is placed below the first ball, the tension in the strings doubles:
T′=2T
The new tension is 2T.
The new equilibrium condition considering the electrostatic force Fe between the two charges is:
4Tcos(30∘)=mg+Fe
Substituting Fe=14πϵ0q2r2 where r=4.2×10−2m:
4T(√32)=mg+14πϵ0q2(4.2×10−2)2
This simplifies to:
2T√3=mg+14πϵ0q2(4.2×10−2)2
From the previous steps, we know:
2T=2(mg√3)
Substituting this into the equation:
2(mg√3)√3=mg+14πϵ0q2(4.2×10−2)2
This simplifies to:
2mg=mg+14πϵ0q2(4.2×10−2)2
mg=14πϵ0q2(4.2×10−2)2
Rearranging gives:
q2=mg⋅(4.2×10−2)2⋅4πϵ0
Substituting ϵ0=8.85×10−12C2/N m2:
q2=(5.88×10−4⋅9.8)⋅(4.2×10−2)2⋅4π(8.85×10−12)
Calculating q2:
q2=(5.76×10−3)⋅(1.764×10−3)⋅(1.112×10−10)
q2≈1.1×10−15
Thus,
q≈√1.1×10−15≈3.3×10−8C
- The charge on the ball is approximately q≈3.3×10−8C.
- The new tension in the strings is T′=2T≈6.64×10−3N.
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Part - II
Explore 23 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
A bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
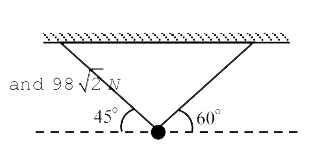
View SolutionA 10 kg steel ball is suspended by two strings as shown. The tensions in the two strings are: (g=9.8 m/s2)
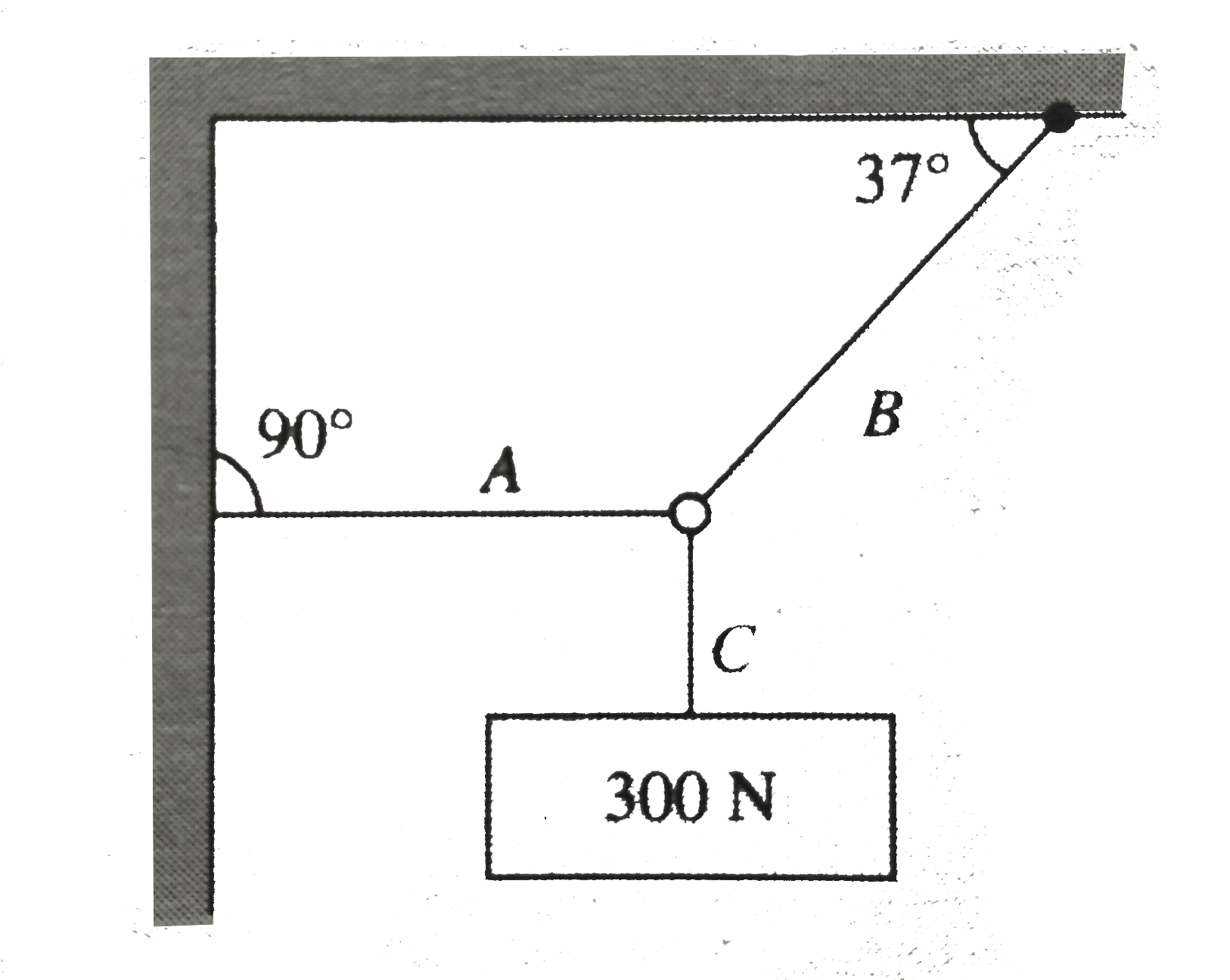
View SolutionA block of mass 30 kg is suspended by three string as shown in fig, Find the tension in each string.
View SolutionA 5.5 m length of string has a mass of 0.035 kg. If the tension in the string is 77 N the speed of a wave on the string is
View SolutionA block of mass 10 kg is suspended by three strings as shown in figure . Tension T2 is

View SolutionA mass of 10 kg is suspended from a spring balance. It is pulled aside by a horizontal string so that it makes an angle of 60∘ with the vertical. The new rading of the balance is
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View Solution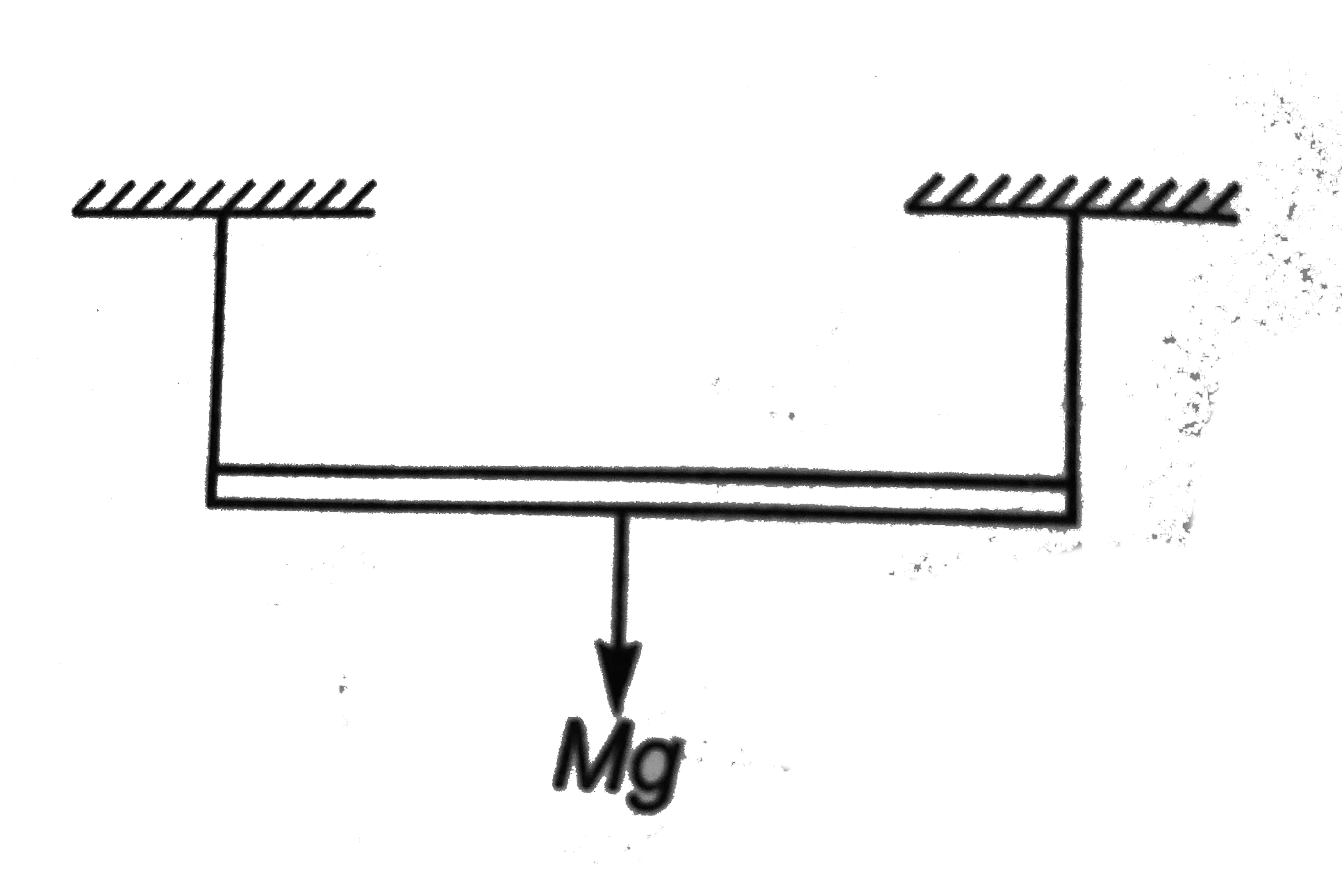
A rod is supported horizontally by means of two strings of equal length as shown in figure. If one of the string is cut. Then tension in other string at the same instant will.
View SolutionTwo path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
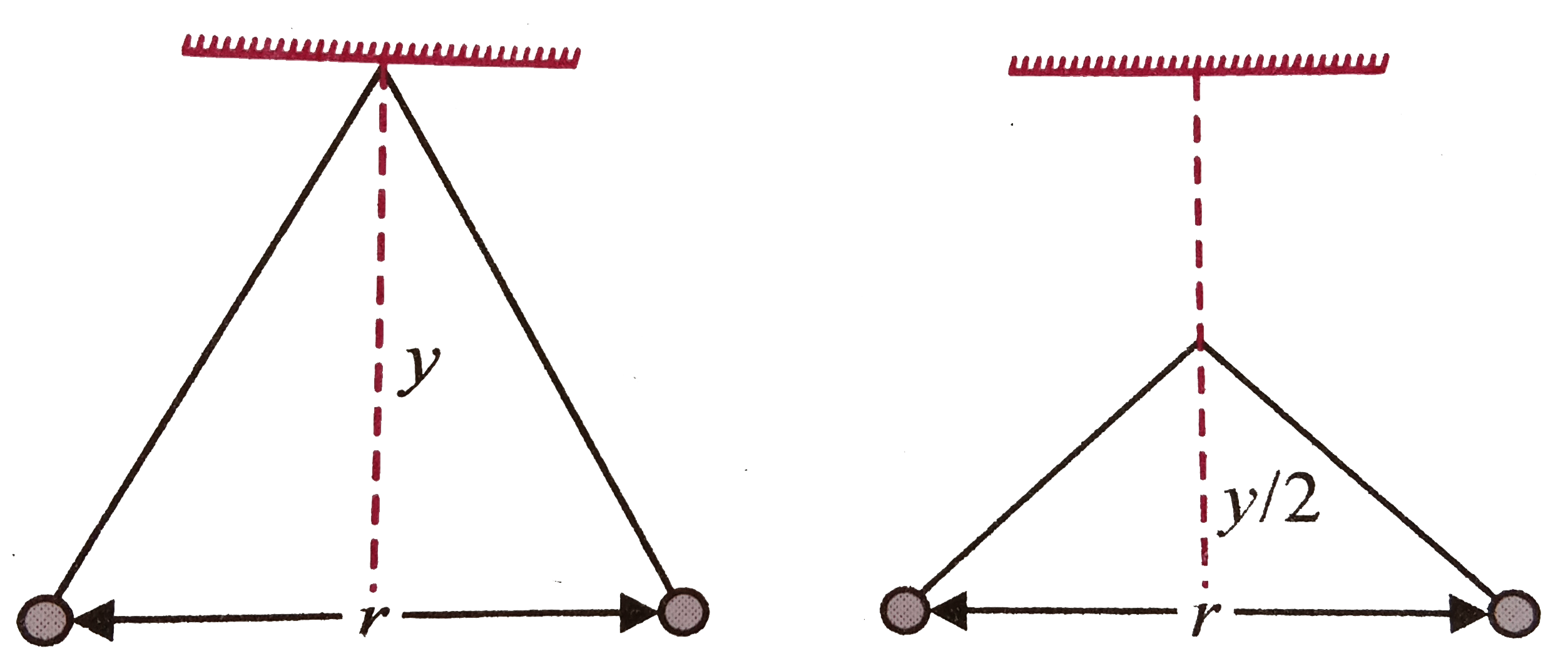
View SolutionTwo charged particles having charge 2.0×10−8C each are joined by an insulating string of length 1 m and the system is kept on a smooth horizontal table. Find the tension in the string.
View Solution