Six equal point charges q0 each are placed at six corners of a regular hexagon of side 'a'. Find out work required o take a point charge 'q' slowly :
(i) From infinity to the centre of haxagon.
(ii) From infinity to a point on the axis which is at a distance '√3a' from the centre of hexagon.
(iii) Does your answer to part (i) and (ii) depends on the path followed by the charge.
The correct Answer is:(i) 6Kqq0a (ii) 3Kqq0a (iii) No
To solve the problem step by step, we will analyze each part of the question systematically.
Given:
- Six equal point charges q0 are placed at the corners of a regular hexagon with side length a.
- We need to find the work done to bring a point charge q from infinity to two different locations: the center of the hexagon and a point on the axis at a distance √3a from the center.
Part (i): Work done to bring charge q to the center of the hexagon
1. Determine the potential at the center of the hexagon:
- The potential V at a point due to a point charge is given by:
V=kQr
- For six charges q0 at the corners of the hexagon, the distance from each charge to the center (O) is a√3 (using geometry of the hexagon).
- Therefore, the total potential VO at the center is:
VO=k⎛⎜⎝q0a√3+q0a√3+q0a√3+q0a√3+q0a√3+q0a√3⎞⎟⎠=6kq0√3a
2. Calculate work done:
- The work done W to bring the charge q from infinity (where potential V∞=0) to the center is given by:
W=q(VO−V∞)=q(6kq0√3a−0)=6kqq0√3a
Part (ii): Work done to bring charge q to a point on the axis at distance √3a
1. Determine the potential at the point on the axis:
- The distance from the center of the hexagon to this point is √3a.
- The potential VP at this point due to the six charges is:
VP=k(q0√3a+q0√3a+q0√3a+q0√3a+q0√3a+q0√3a)=6kq0√3a
2. Calculate work done:
- The work done W to bring the charge q from infinity to this point is:
W=q(VP−V∞)=q(6kq0√3a−0)=6kqq0√3a
Part (iii): Dependence of work done on the path
- The work done in moving a charge in an electric field depends only on the initial and final positions, not on the path taken. This is because the electric field is conservative.
- Therefore, the answer to part (i) and part (ii) does not depend on the path followed by the charge.
Summary of Results:
1. Work done to bring charge q to the center:
W1=6kqq0√3a
2. Work done to bring charge q to the point on the axis:
W2=6kqq0√3a
3. The work done does not depend on the path followed.
- Six equal point charges q0 are placed at the corners of a regular hexagon with side length a.
- We need to find the work done to bring a point charge q from infinity to two different locations: the center of the hexagon and a point on the axis at a distance √3a from the center.
- The potential V at a point due to a point charge is given by:
V=kQr
- For six charges q0 at the corners of the hexagon, the distance from each charge to the center (O) is a√3 (using geometry of the hexagon).
- Therefore, the total potential VO at the center is:
VO=k⎛⎜⎝q0a√3+q0a√3+q0a√3+q0a√3+q0a√3+q0a√3⎞⎟⎠=6kq0√3a
- The work done W to bring the charge q from infinity (where potential V∞=0) to the center is given by:
W=q(VO−V∞)=q(6kq0√3a−0)=6kqq0√3a
- The distance from the center of the hexagon to this point is √3a.
- The potential VP at this point due to the six charges is:
VP=k(q0√3a+q0√3a+q0√3a+q0√3a+q0√3a+q0√3a)=6kq0√3a
- The work done W to bring the charge q from infinity to this point is:
W=q(VP−V∞)=q(6kq0√3a−0)=6kqq0√3a
- Therefore, the answer to part (i) and part (ii) does not depend on the path followed by the charge.
1. Work done to bring charge q to the center:
W1=6kqq0√3a
2. Work done to bring charge q to the point on the axis:
W2=6kqq0√3a
3. The work done does not depend on the path followed.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (D)
5 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (E)
2 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (B)
12 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
Knowledge Check
Four equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
AzeroB√2q2πε0aC√2qπε0aDq2πε0aSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
AGm2l2[54+1√3]BGm2l2[34+1√3]CGm2l2[54−1√3]DGm2l2[34−1√3]
Five point charges each of charge +q are placed on five vertices of a regular hexagon of side h as shown in the figure. Then
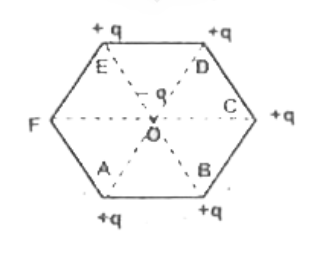
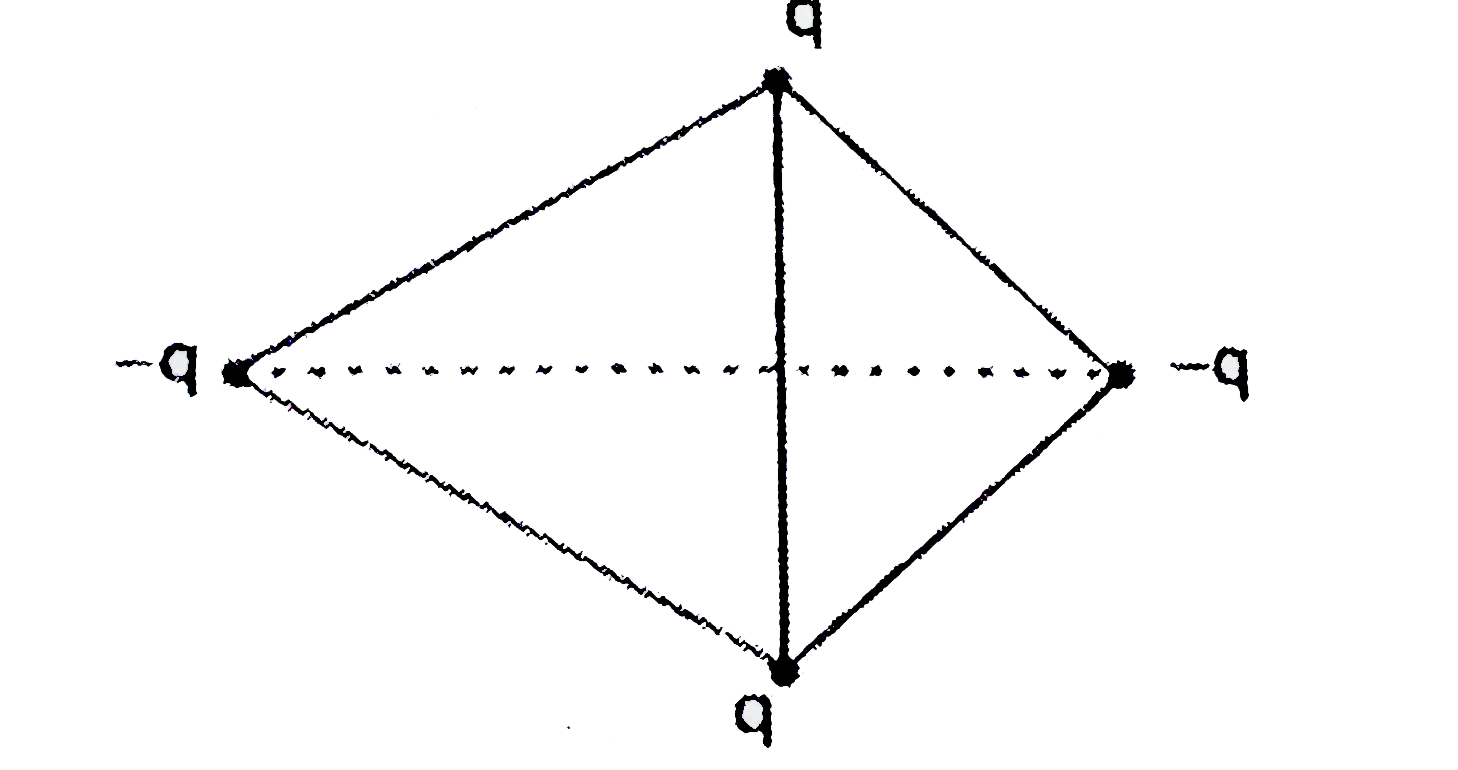
View SolutionFour small point charges (each of equal magnitude q) are placed at four corners of a regular tetrahedron of side a. find out potential energy of charge system
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionFive point charge (+q each) are placed at the five vertices of a regular hexagon of side 2a.what is the magnitude of the net electric field at the centre of the hexazon?
View SolutionSix point masses of mass m each are at the vertices of a regular hexagon of side l. Calculate the force on any of the masses.
View SolutionA charge Q is placed at each corner of a cube of side a. The potential at the centre of the cube is
View Solution


