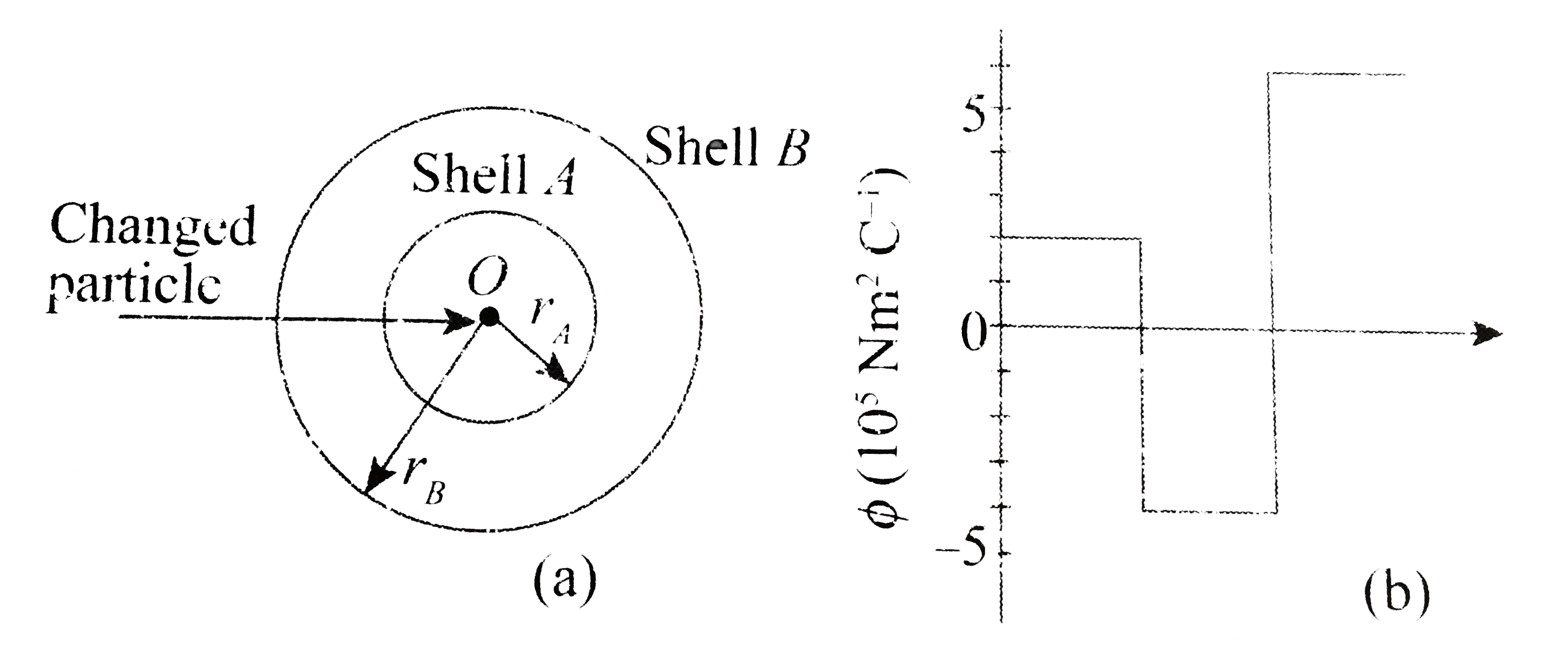
A charged particle is suspended at the center of two thin concentric spherical charged shells, made of nonconducting material. Figure shows cross section of the arrangement. Figure (b) gives the net flux ϕ through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere.
 ,
,
In which range of the values of r is the electric field zero?
0 to rA
rA to rB
For r>rB
For no range of r, electric field is zero.
The correct Answer is:D
Step by step video & image solution for A charged particle is suspended at the center of two thin concentric spherical charged shells, made of nonconducting material. Figure shows cross section of the arrangement. Figure (b) gives the net flux phi through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere. , In which range of the values of r is the electric field zero? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Exercise - 3 Part - I33videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Part - II23videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - Part- II20videos
ELECTROSTATICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
- BOOK - RESONANCE ENGLISHCHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II10videos
EXPERIMENTAL PHYSICS
Similar Questions
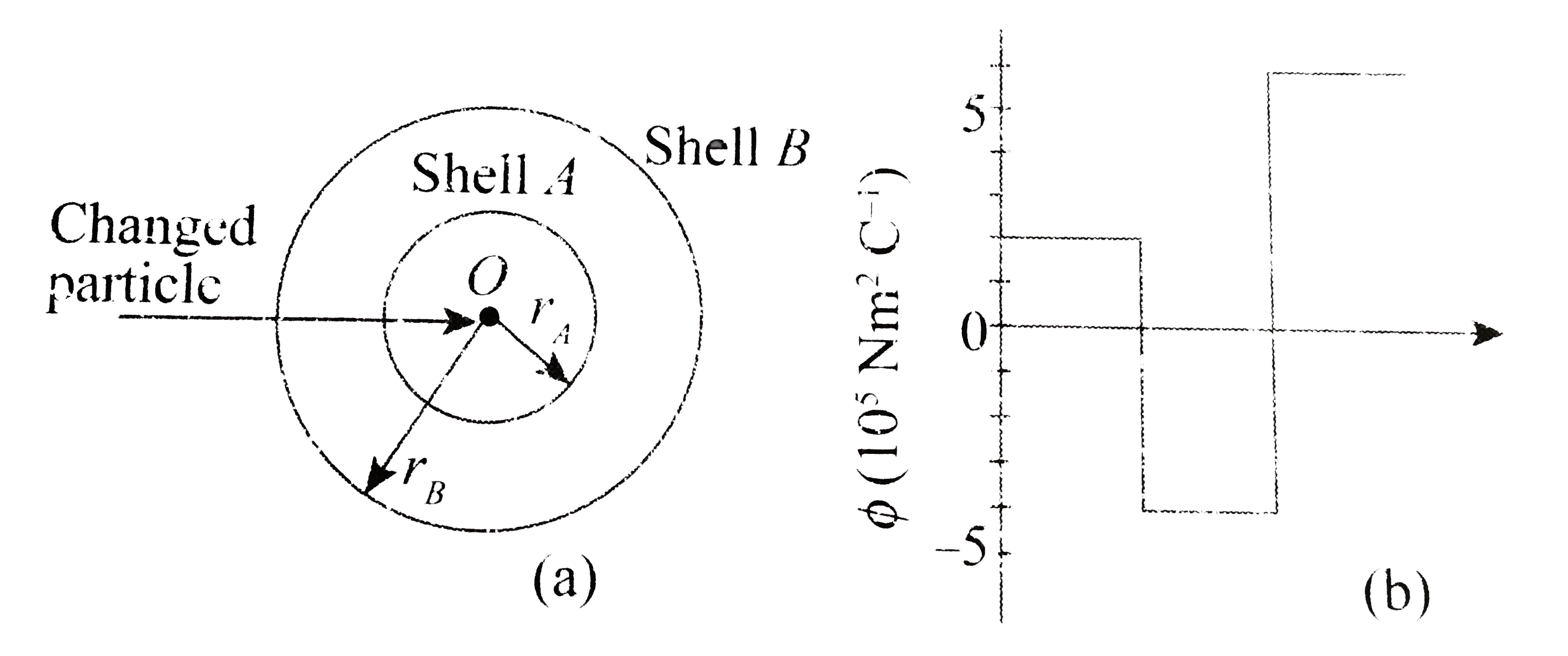
A charged particle is suspended at the center of two thin concentric spherical charged shells, made of nonconducting material. Figure shows cross section of the arrangement. Figure (b) gives the net flux ϕ through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere.
 ,
,
What is the charge on shell A?View SolutionA charged particle is suspended at the center of two thin concentric spherical charged shells, made of nonconducting material. Figure shows cross section of the arrangement. Figure (b) gives the net flux ϕ through a Gaussian sphere centered on the particle, as a function of the radius r of the sphere.
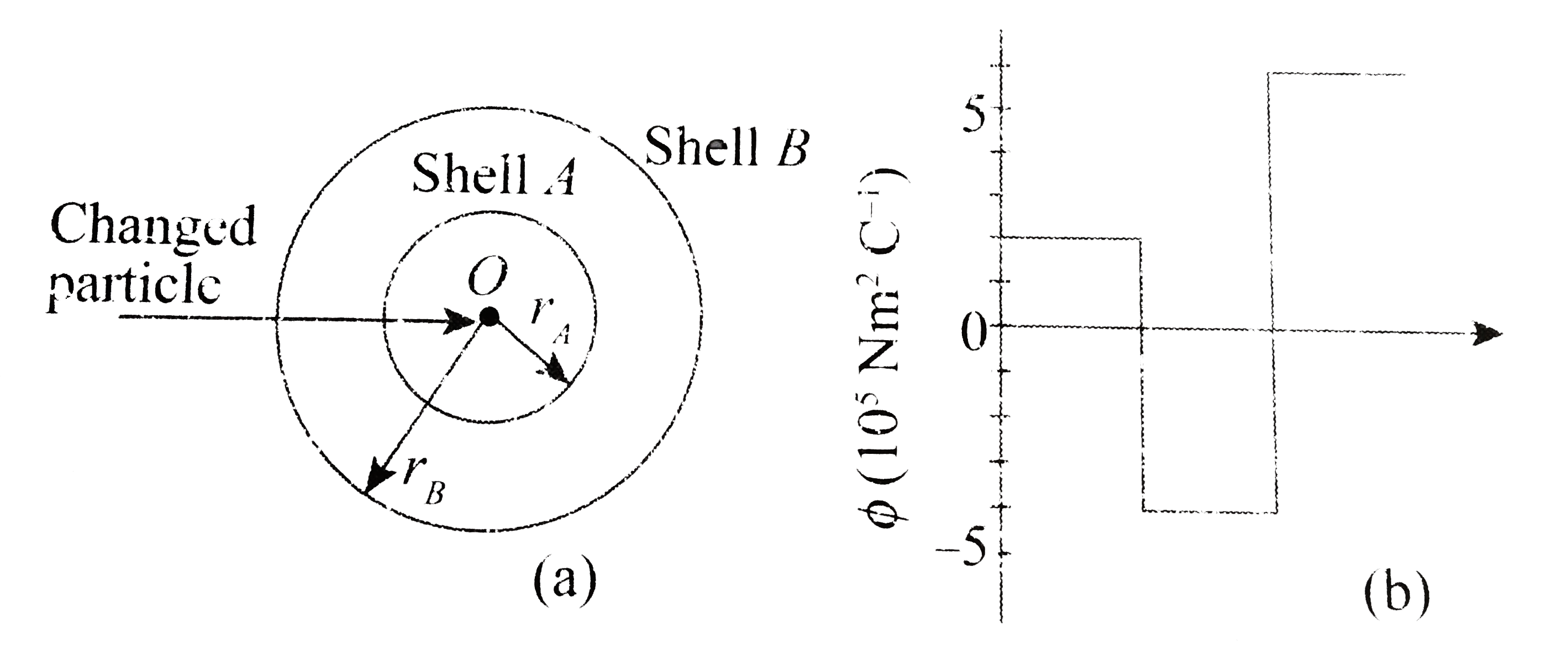 ,
,
What is the charge on the central particle?View SolutionA non-conducting spherical shell of radius R surrounds a point charge q (q at center). The electric flux through a cap of the shell of half angle θ is:
View SolutionA non-conducting spherical shell of radius R surrounds a point charge q (q at center). The electric flux through a cap of the shell of half angle θ is:
View SolutionA charged particle is held a the centre foa sperical shell. The following figure gives the magnitude E of the electric field versus radial distance r. what is the net charge on the shell ?
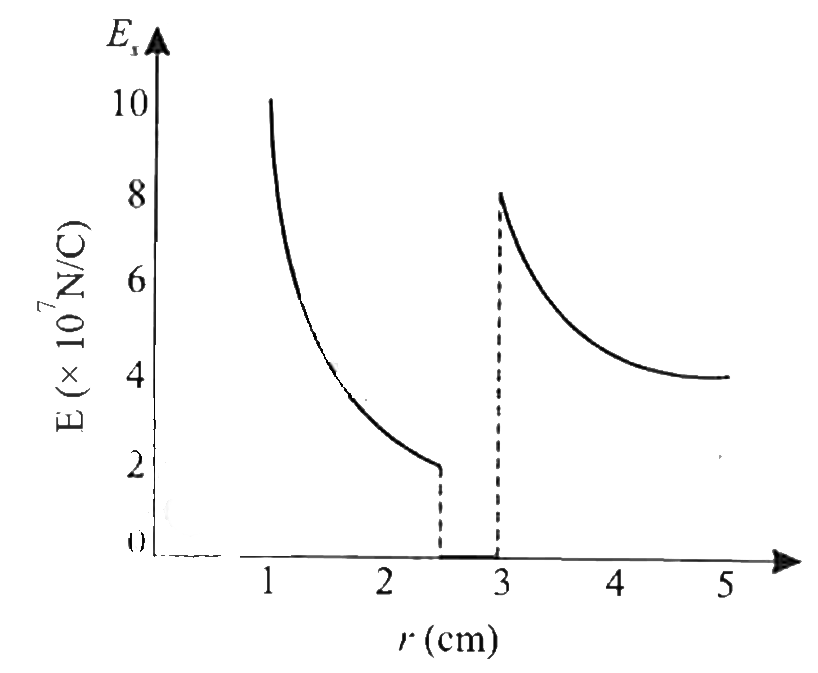 View Solution
View SolutionAn infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surface of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surface is .
 View Solution
View SolutionGraph shows magnitude of electric field (E), charge enclosed (qenclosed⟩) within the concentic sphere and net flux (ϕ) through a concentric spherical Gaussian surface as a function of distance (r) from centre of a uniformly positive charged solid sphere of radius R. Choose the correct option (s):
View Solutionfigure shows, in cross section, two Gaussian spheres and two Gaussian cubes that are centered on a positively charged particle on a positively charged partical . Rank greatest first, and indicate whether the manitudes are unifrom or variable along each surface.
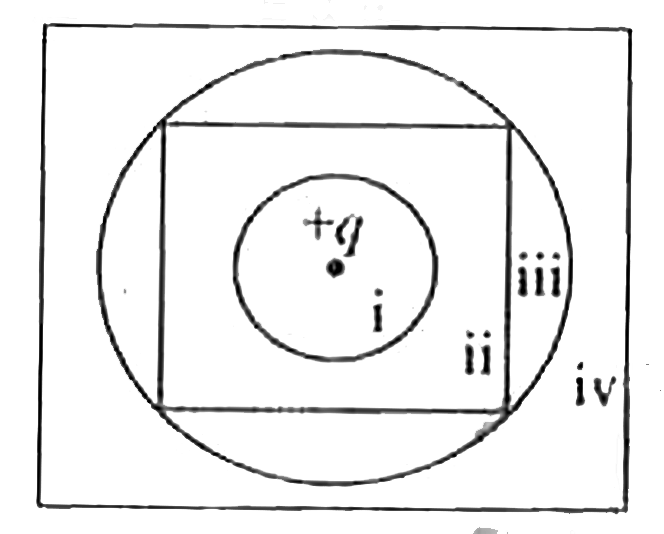 View Solution
View SolutionA conducting sphere of radius R and a concentric thick spherical shell of inner radius 2R and outer radius 3R is shown in figure. A charge +10Q is given to the shell and inner sphere is earthed. Then charge on inner sphere is
 View Solution
View SolutionThe region between two concentric spheres of radii 'a' and 'b', respectively (see figure), have volume charge density ρ=Ar, where A is a constant and r is the distance from the centre. At the centre of the spheres is a point charge Q. The value of A such that the electric field in the region between the spheres will be constant, is:
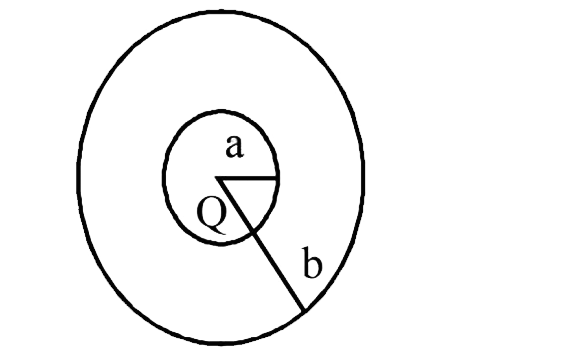 View Solution
View Solution

