A particle of charge -q and mass m moves in a circular orbit about a fixed charge +Q. Show that the r3αT2 law, is satisfied, where r is the radius of orbit and T is time period.
To show that r3∝T2 for a particle of charge −q moving in a circular orbit around a fixed charge +Q, we can follow these steps:
Step 1: Identify the Forces Acting on the Particle
The particle of charge −q experiences a Coulombic force due to the fixed charge +Q. This force acts as the centripetal force required for circular motion.
Step 2: Write the Expression for Coulomb's Law
The magnitude of the Coulombic force Fe between the two charges is given by:
Fe=k⋅|q|⋅|Q|r2
where k is Coulomb's constant, q is the charge of the particle, Q is the fixed charge, and r is the radius of the orbit.
Step 3: Set the Coulombic Force Equal to the Centripetal Force
For circular motion, the required centripetal force Fc is given by:
Fc=mv2r
where m is the mass of the particle and v is its linear velocity.
Since the Coulombic force provides the centripetal force, we can set them equal:
k⋅|q|⋅|Q|r2=mv2r
Step 4: Relate Linear Velocity to Angular Velocity
The linear velocity v can be related to the angular velocity ω by the equation:
v=ωr
Substituting this into the centripetal force equation gives:
k⋅|q|⋅|Q|r2=m(ωr)2r
This simplifies to:
k⋅|q|⋅|Q|r2=mω2r
Step 5: Express Angular Velocity in Terms of Time Period
The angular velocity ω is related to the time period T by:
ω=2πT
Substituting this into the equation gives:
k⋅|q|⋅|Q|r2=m(2πT)2r
Step 6: Rearrange the Equation
Rearranging the equation leads to:
k⋅|q|⋅|Q|=m(2π)2T2r3
This can be expressed as:
r3=k⋅|q|⋅|Q|m⋅(2π)2T2
Conclusion
From the equation r3=k⋅|q|⋅|Q|m⋅(2π)2T2, we see that r3 is proportional to T2:
r3∝T2
The particle of charge −q experiences a Coulombic force due to the fixed charge +Q. This force acts as the centripetal force required for circular motion.
The magnitude of the Coulombic force Fe between the two charges is given by:
Fe=k⋅|q|⋅|Q|r2
where k is Coulomb's constant, q is the charge of the particle, Q is the fixed charge, and r is the radius of the orbit.
For circular motion, the required centripetal force Fc is given by:
Fc=mv2r
where m is the mass of the particle and v is its linear velocity.
k⋅|q|⋅|Q|r2=mv2r
The linear velocity v can be related to the angular velocity ω by the equation:
v=ωr
Substituting this into the centripetal force equation gives:
k⋅|q|⋅|Q|r2=m(ωr)2r
This simplifies to:
k⋅|q|⋅|Q|r2=mω2r
The angular velocity ω is related to the time period T by:
ω=2πT
Substituting this into the equation gives:
k⋅|q|⋅|Q|r2=m(2πT)2r
Rearranging the equation leads to:
k⋅|q|⋅|Q|=m(2π)2T2r3
This can be expressed as:
r3=k⋅|q|⋅|Q|m⋅(2π)2T2
From the equation r3=k⋅|q|⋅|Q|m⋅(2π)2T2, we see that r3 is proportional to T2:
r3∝T2
Topper's Solved these Questions
- ELECTROSTATICSBook:RESONANCE ENGLISHChapter:ELECTROSTATICSExercise:Part - II
Explore 23 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
- EXPERIMENTAL PHYSICSBook:RESONANCE ENGLISHChapter:EXPERIMENTAL PHYSICSExercise:PART -II
Explore 10 Videos
Similar Questions
A particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View Solution
Knowledge Check
A particle of charge q and mass m moves in a circular orbit of radius r with angular speed w the ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
Aw and qBw, q and mCq and mDw and m
A particle of charge 'q' and mass 'm' move in a circular orbit of radius 'r' with frequency 'v' the ratio of the magnetic moment to angular momentum is:
View SolutionA particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
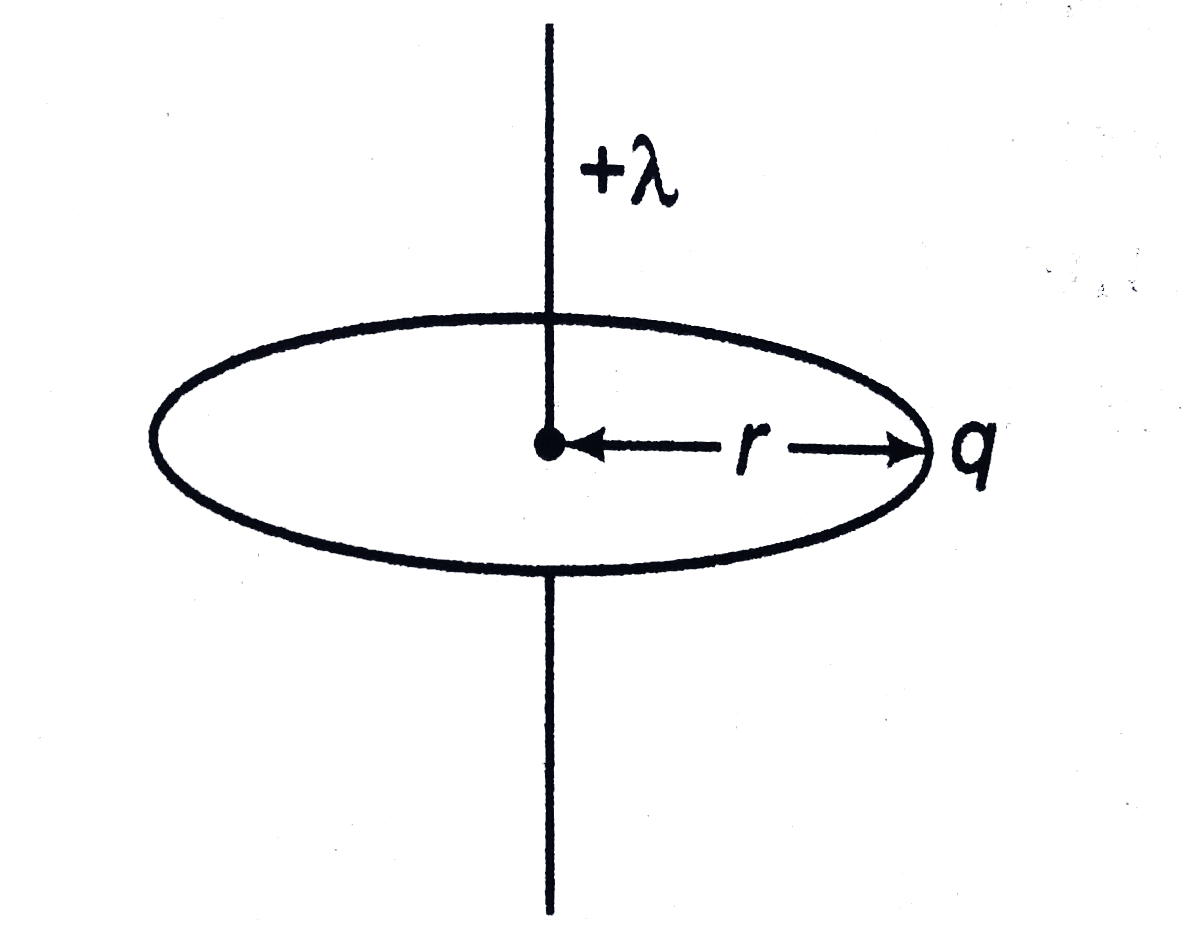 where , k=14πε0)
where , k=14πε0)
View SolutionA proton of mass m and charge +e is moving in a circular orbit in a magnetic field with energy 1MeV. What should be the energy of alpha-particle (mass=4m and charge=+2e), so that it can revolve in the path of same radius?
View SolutionA test particle is moving in a circular orbit in the gravitational field produced by a mass density ρ(r)=Kr2. Indentify the correct relation between the radius R of the particle's orbit and its period T :
View SolutionThe period T0 for a planet of mass 'm' above the sum in a circular orbit of radius R depends on m,R and G where G is the gravitational constant. Find expression for time period by dimensional methods.
View SolutionA charged particle of mass m and charge q travels on a circular path of radius r that is perpendicular to a magnetic field B. The time takeen by the particle to complete one revolution is
View SolutionWhat is the mass of the planet that has a satellite whose time period is T and orbital radius is r?
View Solution