As an electron (at rest) is brought towards a proton from infinity, its
Potential energy increases
Potential energy decreases
Kinetic energy increases
Total energy remains constant
To solve the problem, we need to analyze the behavior of an electron as it moves towards a proton from infinity. Let's break down the steps:
1. Understanding the Initial Conditions:
- The electron is initially at rest and located at an infinite distance from the proton. At this point, the potential energy (PE) is defined as zero.
2. Bringing the Electron Closer:
- As the electron is brought closer to the proton, it experiences an attractive electrostatic force due to the proton. This force is given by Coulomb's law:
F=k⋅|q1⋅q2|r2
- Here, k is Coulomb's constant, q1 is the charge of the proton, q2 is the charge of the electron, and r is the distance between them.
3. Change in Potential Energy:
- The potential energy of the system changes as the electron moves closer to the proton. The potential energy (PE) of the electron-proton system is given by:
PE=−k⋅e2r
- As r decreases (the electron gets closer to the proton), the magnitude of the potential energy becomes larger (more negative), indicating that the potential energy decreases.
4. Kinetic Energy Consideration:
- Since the electron is initially at rest, it has zero kinetic energy (KE) at infinity. As it moves towards the proton, the attractive force causes it to accelerate, which increases its kinetic energy.
- The work done on the electron by the electrostatic force results in an increase in its kinetic energy.
5. Conservation of Energy:
- The total mechanical energy (E) of the system is conserved in the absence of external forces. The total energy is the sum of kinetic energy and potential energy:
E=KE+PE
- As the electron moves closer to the proton, its kinetic energy increases while its potential energy decreases, keeping the total energy constant.
6. Conclusion:
- As the electron approaches the proton, its kinetic energy increases, potential energy decreases, and total energy remains constant.
Final Answer:
- Kinetic Energy Increases: True
- Potential Energy Decreases: True
- Total Energy Remains Constant: True
- The electron is initially at rest and located at an infinite distance from the proton. At this point, the potential energy (PE) is defined as zero.
- As the electron is brought closer to the proton, it experiences an attractive electrostatic force due to the proton. This force is given by Coulomb's law:
F=k⋅|q1⋅q2|r2
- Here, k is Coulomb's constant, q1 is the charge of the proton, q2 is the charge of the electron, and r is the distance between them.
- The potential energy of the system changes as the electron moves closer to the proton. The potential energy (PE) of the electron-proton system is given by:
PE=−k⋅e2r
- As r decreases (the electron gets closer to the proton), the magnitude of the potential energy becomes larger (more negative), indicating that the potential energy decreases.
- Since the electron is initially at rest, it has zero kinetic energy (KE) at infinity. As it moves towards the proton, the attractive force causes it to accelerate, which increases its kinetic energy.
- The work done on the electron by the electrostatic force results in an increase in its kinetic energy.
- The total mechanical energy (E) of the system is conserved in the absence of external forces. The total energy is the sum of kinetic energy and potential energy:
E=KE+PE
- As the electron moves closer to the proton, its kinetic energy increases while its potential energy decreases, keeping the total energy constant.
- As the electron approaches the proton, its kinetic energy increases, potential energy decreases, and total energy remains constant.
- Kinetic Energy Increases: True
- Potential Energy Decreases: True
- Total Energy Remains Constant: True
Topper's Solved these Questions
Similar Questions
A fixed ring of radius R is given a charge q. A charge q0 is brought slowly from infinity to the centre of the ring. The wrong statement is-
View SolutionThe mass of a proton is 1847 times that of an electron A electron and a proton are injected into a unifrom electric field at right angle to the direction of the field with the same initial K.E.
View SolutionAssertion: The centre mass of an electron and proton, when released moves faster towards proton.
Reason: Proton is heavier than electron.View SolutionAssertion: The centre mass of an electron and proton, when released moves faster towards proton.
Reason: Proton is heavier than electron.View SolutionA proton moves from a large distance with a speed u m/s directly towards a free proton originally at rest. Find the distance of closest of closest approach for the two protons in terms of mass of proton m and its charge e.
View SolutionA neutron at rest decays. Assuming the resulting proton to remain at rest, too, find the kinetic energy of the electron and the energy of the antineutrino.
View SolutionAn electron (mass me)falls through a distance d in a uniform electric field of magnitude E.
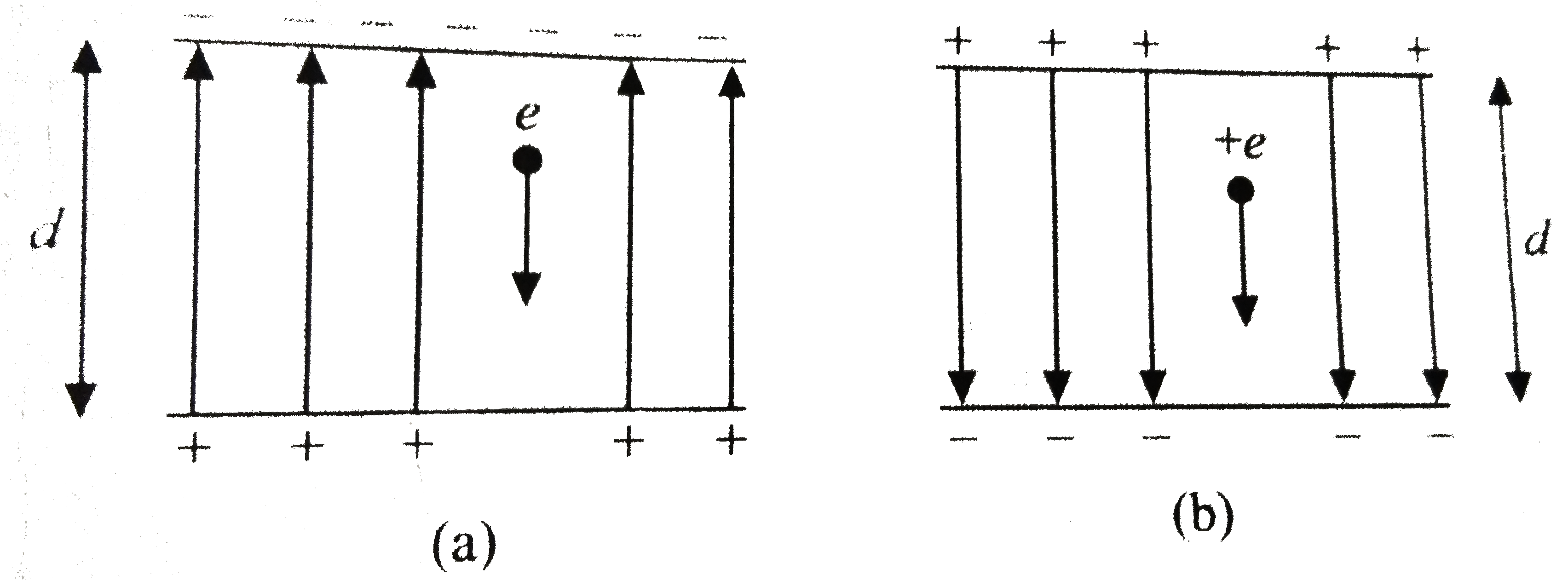 ,
,
The direction of the field is reversed keeping its magnitudes unchanged, and a proton(mass mp) falls through the same distance. If the times taken by the electrons and the protons to fall the distance d is telectron and tproton respectively, then the ratio telectron/tproton.View SolutionA point charge q is brought slowly from infinity and is placed at the centre of a conducting neutral spherical shell of inner radius a and outer radius b, then find work done by external agent :
 View Solution
View SolutionAn electron is revolving around a proton. The total work done in one revolution by electric force on the electron will be zero if the trajectory of the electron is
View SolutionAn electron is revolving around a proton. The total work done in one revolution by electric force on the electron will be zero if the trajectory of the electron is
View Solution

