Air in a room is separated in two regions in volume ratio of 4: 1 by an imaginary boundary. Which statement is correct
Mavg of air in bigger region is half of Mavg of air in smaller region
Mavg of air in bigger region is twice of Mavg of air in smaller region
Both regions ill have same Mavg of air.
Mavg of air in bigger region is thrice of Mavg of air in smaller region
To solve the problem, we need to analyze the situation where air in a room is divided into two regions with a volume ratio of 4:1. We will determine the correct statement regarding the mass of air in these two regions.
1. Understanding the Volume Ratio:
- The volume of the larger region (V1) is 4 parts, and the volume of the smaller region (V2) is 1 part. Therefore, we can express the volumes as:
- V1 = 4x
- V2 = x
- The total volume (V_total) = V1 + V2 = 4x + x = 5x.
2. Using the Ideal Gas Law:
- According to the ideal gas law, PV=nRT, where:
- P = pressure,
- V = volume,
- n = number of moles,
- R = universal gas constant,
- T = temperature.
- Since the temperature and pressure are assumed to be constant in both regions, the number of moles (n) is directly proportional to the volume (V).
3. Calculating the Mass of Air:
- The mass of air (m) can be calculated using the formula:
- m=n×M
- where M is the molar mass of air.
- Since the number of moles is proportional to the volume, we can say:
- n1∝V1 and n2∝V2
- Therefore, the mass in each region can be expressed as:
- m1=n1×M and m2=n2×M
4. Finding the Mass Ratio:
- Since n1 and n2 are proportional to V1 and V2:
- n1=k⋅V1=k⋅4x
- n2=k⋅V2=k⋅x
- The mass in each region will then be:
- m1=k⋅4x⋅M
- m2=k⋅x⋅M
- The ratio of the masses is:
- m1m2=4kxMkxM=4
5. Conclusion:
- The mass of air in the larger region (m1) is 4 times the mass of air in the smaller region (m2). Therefore, the correct statement is that the average mass of air in the larger region is four times that of the smaller region.
- The volume of the larger region (V1) is 4 parts, and the volume of the smaller region (V2) is 1 part. Therefore, we can express the volumes as:
- V1 = 4x
- V2 = x
- The total volume (V_total) = V1 + V2 = 4x + x = 5x.
- According to the ideal gas law, PV=nRT, where:
- P = pressure,
- V = volume,
- n = number of moles,
- R = universal gas constant,
- T = temperature.
- Since the temperature and pressure are assumed to be constant in both regions, the number of moles (n) is directly proportional to the volume (V).
- The mass of air (m) can be calculated using the formula:
- m=n×M
- where M is the molar mass of air.
- Since the number of moles is proportional to the volume, we can say:
- n1∝V1 and n2∝V2
- Therefore, the mass in each region can be expressed as:
- m1=n1×M and m2=n2×M
- Since n1 and n2 are proportional to V1 and V2:
- n1=k⋅V1=k⋅4x
- n2=k⋅V2=k⋅x
- The mass in each region will then be:
- m1=k⋅4x⋅M
- m2=k⋅x⋅M
- The ratio of the masses is:
- m1m2=4kxMkxM=4
- The mass of air in the larger region (m1) is 4 times the mass of air in the smaller region (m2). Therefore, the correct statement is that the average mass of air in the larger region is four times that of the smaller region.
Topper's Solved these Questions
Similar Questions
Although, nitrogen does not adsorb on a surface at room temperature, it adsorbs on the surface at 83 K. Which one of the following statements is correct?
View SolutionConsider the following statements
A marathon runner is likely to show
1. Reduced heart rate
2. Enlarged heart
3. larger stroke volume
4. Decreased arterial blood pressure
Which of the above statement is/are correct?
View SolutionThe CFCs are used in refrigerators, air conditioners, in the production of plastic foam etc. Which of the following statements are correct ?
View SolutionA point charge +Q is place just outside an imaginary hemispherical surface of radius R as shown in the figure. Which of the following statements is/are correct ?
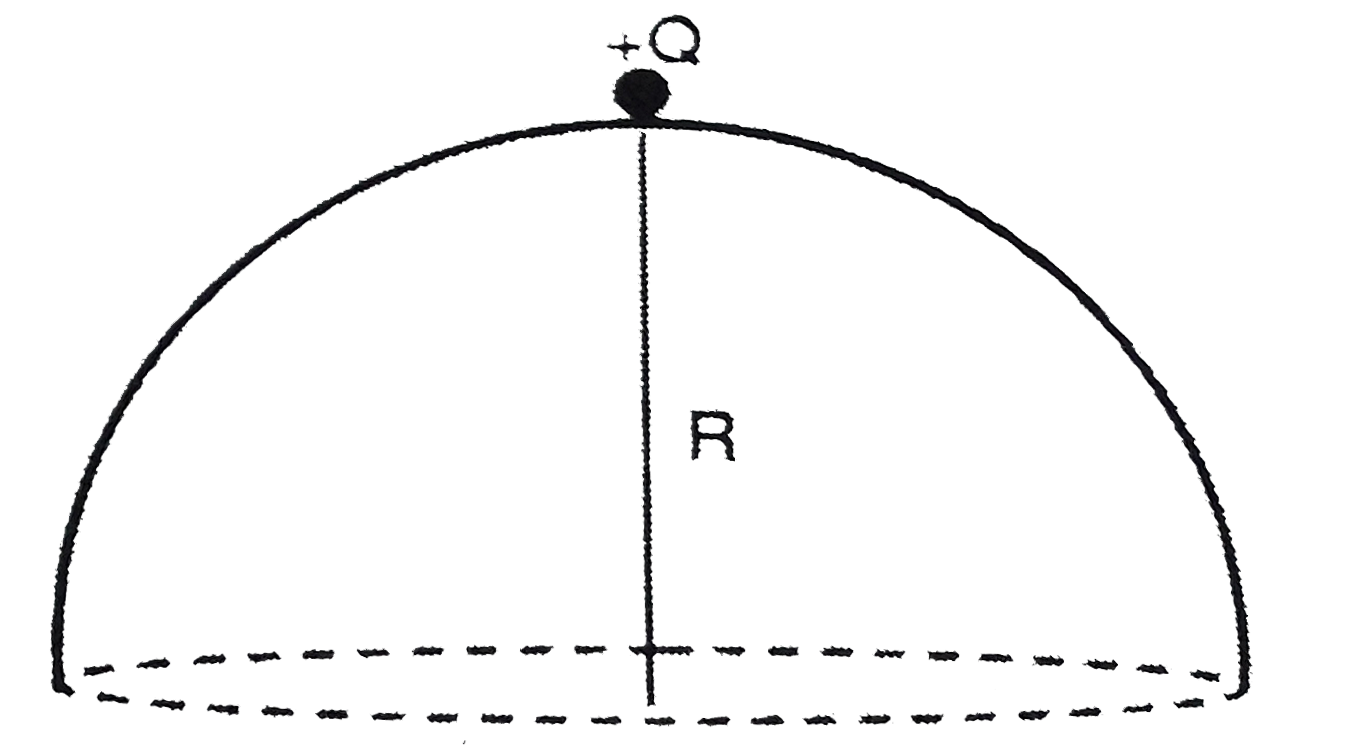
View SolutionIn case of induced electric field due to a time-dependent magnetic field in a cylindrical region, which of the statement is correct?
View SolutionCD2 = CH - CH2−Br is subjected to SN1andSN2 reactions separately, which of the following statement is correct ?
View SolutionA corner point of a feasible region is a point in the reqion which is the of two boundary lines.
View SolutionA parallel plate air capacitor is connected to a battery. After charging fully, the battery is disconnected and the plates are pulled apart to increase their separation. Which of the following statements is correct ?
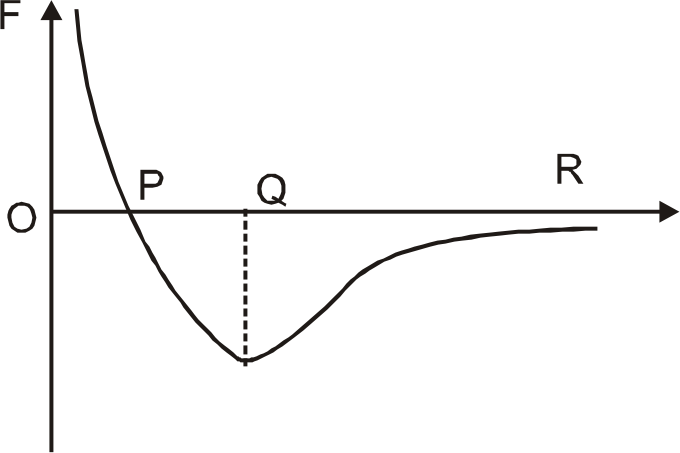
View SolutionFigure shows roughly how the force F between two adjacent atoms in a solid varies with inter atomic separation r. Which of the following statements are correct ?
View SolutionRatio of amplitude for two wave is 1:4 .Find the ratio of intensity?
View Solution
