How many geometrical isomers are possible for Hepta-2, 5-dienoic acid:
The correct Answer is:CH3−HC=CH−CH2−CH=CH−COOH
Four geometrical isomers are possible.
To determine the number of geometrical isomers for Hepta-2,5-dienoic acid, we can follow these steps:
Step 1: Understand the Structure of Hepta-2,5-dienoic Acid
Hepta-2,5-dienoic acid has the following structure:
- It has a total of 7 carbon atoms (hence "hepta").
- There are double bonds between carbon atoms at positions 2 and 3, and at positions 5 and 6.
Step 2: Identify the Double Bonds
In Hepta-2,5-dienoic acid, there are two double bonds:
- C2=C3
- C5=C6
Step 3: Determine Conditions for Geometrical Isomerism
Geometrical isomerism (cis-trans isomerism) occurs due to restricted rotation around double bonds. For a compound to exhibit geometrical isomerism:
- Each carbon involved in the double bond must have different substituents.
Step 4: Analyze Each Double Bond
1. For the first double bond (C2=C3):
- C2 has two substituents: one is a hydrogen (H) and the other is part of the carbon chain.
- C3 also has two substituents: one is a hydrogen (H) and the other is part of the carbon chain.
- Since both carbons have different substituents, this double bond can exhibit cis and trans isomerism.
2. For the second double bond (C5=C6):
- C5 has two substituents: one is a hydrogen (H) and the other is part of the carbon chain.
- C6 also has two substituents: one is a hydrogen (H) and the other is part of the carbon chain.
- Similarly, this double bond can also exhibit cis and trans isomerism.
Step 5: Count the Total Geometrical Isomers
- Each double bond can exist in two forms (cis and trans).
- Therefore, for the two double bonds, the total number of geometrical isomers can be calculated as:
- For C2=C3: 2 isomers (cis and trans)
- For C5=C6: 2 isomers (cis and trans)
Thus, the total number of geometrical isomers = 2 (from C2=C3) × 2 (from C5=C6) = 4.
Final Answer
The total number of geometrical isomers possible for Hepta-2,5-dienoic acid is 4.
---
Hepta-2,5-dienoic acid has the following structure:
- It has a total of 7 carbon atoms (hence "hepta").
- There are double bonds between carbon atoms at positions 2 and 3, and at positions 5 and 6.
In Hepta-2,5-dienoic acid, there are two double bonds:
- C2=C3
- C5=C6
Geometrical isomerism (cis-trans isomerism) occurs due to restricted rotation around double bonds. For a compound to exhibit geometrical isomerism:
- Each carbon involved in the double bond must have different substituents.
1. For the first double bond (C2=C3):
- C2 has two substituents: one is a hydrogen (H) and the other is part of the carbon chain.
- C3 also has two substituents: one is a hydrogen (H) and the other is part of the carbon chain.
- Since both carbons have different substituents, this double bond can exhibit cis and trans isomerism.
- C5 has two substituents: one is a hydrogen (H) and the other is part of the carbon chain.
- C6 also has two substituents: one is a hydrogen (H) and the other is part of the carbon chain.
- Similarly, this double bond can also exhibit cis and trans isomerism.
- Each double bond can exist in two forms (cis and trans).
- Therefore, for the two double bonds, the total number of geometrical isomers can be calculated as:
- For C2=C3: 2 isomers (cis and trans)
- For C5=C6: 2 isomers (cis and trans)
The total number of geometrical isomers possible for Hepta-2,5-dienoic acid is 4.
Topper's Solved these Questions
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART 1 SECTION (J))
6 Videos
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART 1 SECTION (K))
2 Videos
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART 1 SECTION (H))
2 Videos
- SOLUTIONSBOOK - RESONANCE ENGLISHCHAPTER - SOLUTIONSEXERCISE - Advabced Level Problems (PART-2)
35 Videos
- STRUCTURAL IDENTIFICATIONBOOK - RESONANCE ENGLISHCHAPTER - STRUCTURAL IDENTIFICATIONEXERCISE - Advanced level Problems (Part-III)
12 Videos
Similar Questions
Knowledge Check
CH2=CH–CH=CH–CH=CH2
How many geometrical isomers are possible for this compound ?A2B3C4D8CH3−CH=C∣Br−C∣Cl−CH−CH3
How many geometrical isomers are possible for this compound?A2B3C4D6How many geometrical isomers are possible for the given compound?
CH3−CH=CH−CH=CH−C2H5AFourBThreeCTwoDFive
Number of geometrical isomers possible of
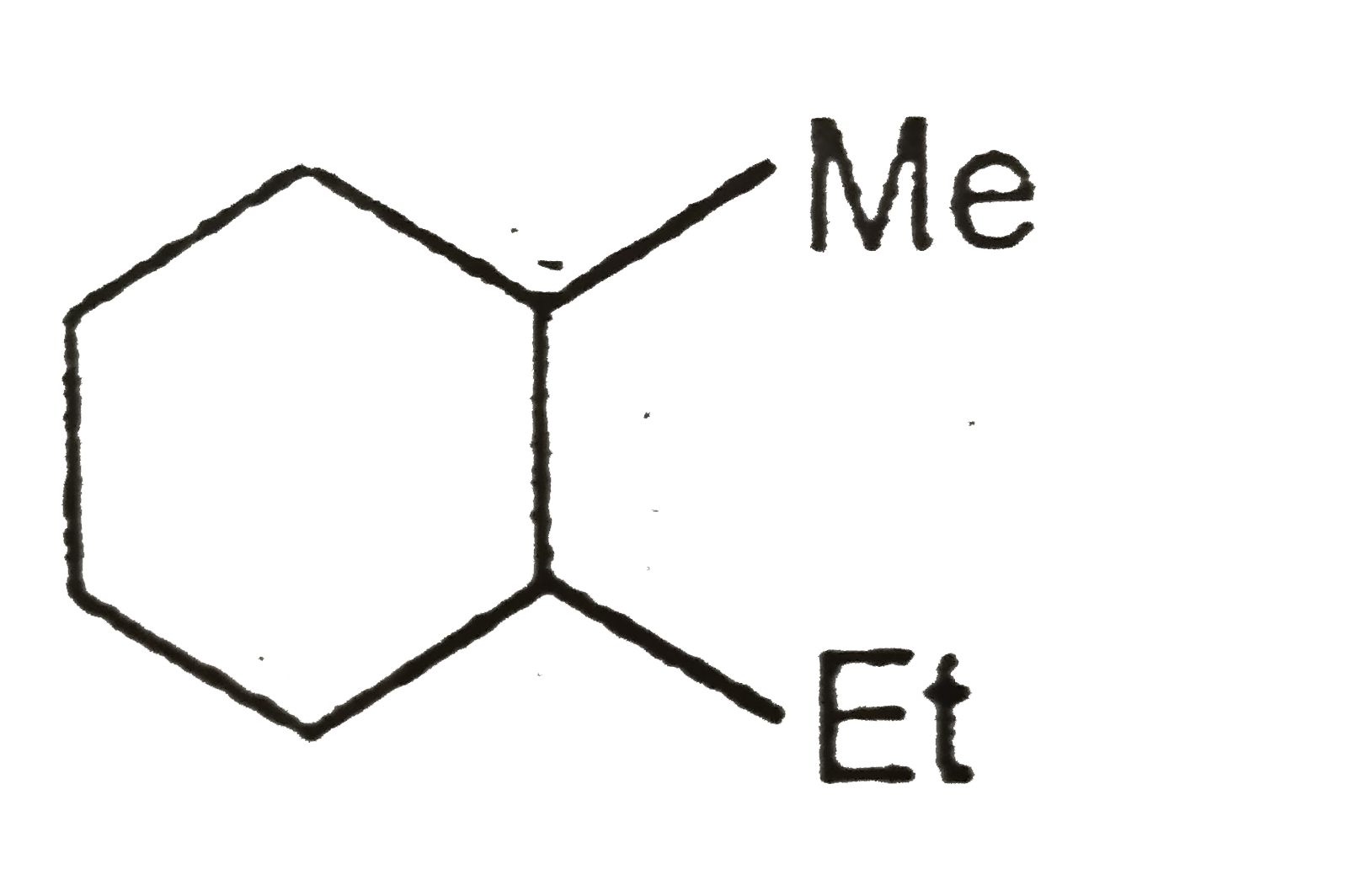
View SolutionHow many geometrical isomers are possible for 1,2,4-Trimethyl cyclohexane.
View SolutionHow many geometrical isomers are possible for the given compound?
Ph-CH=CH-CH=CH-COOH
View SolutionHow many geometrical isomers are possible for the following?
a. Decalin b. 1− Methyldecalin
c. 9− Methyldecalin
View Solutionhow many structural isomers are possible for C6H14?
View Solution