Question

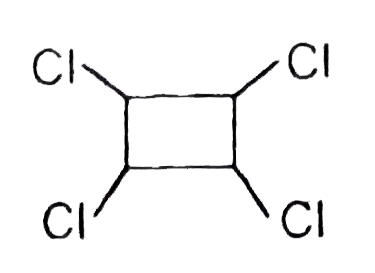
For the given compound ${\displaystyle C{H}_3-\underset{\stackrel{\mid }{OH}}{CH}-CH=CH-C{H}_3.}$
(i) Total number of stereoisomers.
(ii) Number of opticallly active stereoisomers.
(iii) Total number of fractions on fractional distillation of all stereoisomers.

Answer

(I) `CH_(3)-underset(overset(|)(OH))(C)H-CH=CH-CH_(3)`
Number of stereocentres = 2 so total number of stereoisomers = `2^(2)` = 4
(II) All 4 isomers are optically active. (III) Total enantiomeric pairs are 2, hence number of fraction will be 2.

Explanation

To solve the question regarding the compound $CH₃-CH\left(OH\right)-CH=CH-CH₃$, we will break it down into three parts as requested:

Step 1: Total Number of Stereoisomers

1. Identify the Structure: The compound has a double bond between carbon atoms, which allows for geometrical isomerism (cis/trans isomerism).
2. Identify the Double Bond: The double bond is located between the second and third carbon atoms (C2=C3).
3. Geometrical Isomers: For the double bond to have geometrical isomers, the groups attached to the double-bonded carbons must be different. In this case:
- For C2 (attached to OH and CH₃) and C3 (attached to H and CH₂), we can have:
- Cis Isomer: OH and CH₃ on the same side.
- Trans Isomer: OH and CH₃ on opposite sides.
4. Count the Isomers: Since there is one double bond that can exhibit cis/trans isomerism, we can have 2 geometrical isomers.
5. Consider Other Stereoisomers: Additionally, we need to check for any chiral centers. In this compound, there is one chiral center at C2 (attached to OH, CH₃, H, and CH).
6. Total Stereoisomers Calculation: The total number of stereoisomers can be calculated using the formula:
\( \text{Total Stereoisomers} = 2^n \text{ (where n is the number of chiral centers)} \times \text{(number of geometrical isomers)} \)
Here, \( n = 1 \) (one chiral center) and we have 2 geometrical isomers. Thus:
\( \text{Total Stereoisomers} = 2^1 \times 2 = 4 \)

Step 2: Number of Optically Active Stereoisomers

1. Identify Chiral Centers: As previously mentioned, we have one chiral center at C2.
2. Optically Active Isomers Calculation: The number of optically active stereoisomers can be calculated using the formula:
\( \text{Optically Active Isomers} = 2^n \)
Where \( n \) is the number of chiral centers. Since \( n = 1 \):
\( \text{Optically Active Isomers} = 2^1 = 2 \)

Step 3: Total Number of Fractions on Fractional Distillation

1. Identify Enantiomeric Pairs: The optically active isomers are enantiomers (mirror images of each other). Since we have 2 optically active stereoisomers, we have 1 pair of enantiomers.
2. Total Fractions Calculation: The number of fractions obtained from fractional distillation is equal to the number of enantiomeric pairs. Thus:
\( \text{Total Fractions} = 1 \text{ (pair of enantiomers)} \)

Final Answers:
(i) Total number of stereoisomers: 4
(ii) Number of optically active stereoisomers: 2
(iii) Total number of fractions on fractional distillation of all stereoisomers: 2

---