(+) tartaric acid has a specific rotation of +12 unit when measured in 12cm polarimeter tube and 2g/ml concentration at given temperature and light. When it is diluted to half the concentration, length of tube and other parameters being same, then the specific rotation will be:
+6 unit
+12 unit
−6 unit
+24 unit
The correct Answer is:B
To solve the problem regarding the specific rotation of (+) tartaric acid when diluted to half its concentration, we will follow these steps:
Step 1: Understand the formula for specific rotation
The specific rotation (α) is defined by the formula:
(α)=αC⋅L
where:
- α = observed rotation (in degrees)
- C = concentration (in g/mL)
- L = length of the polarimeter tube (in dm)
Step 2: Identify the initial conditions
From the problem statement:
- The specific rotation (α) is given as +12 units.
- The concentration C is 2 g/mL.
- The length L of the polarimeter tube is 12 cm (which is 1.2 dm).
Step 3: Calculate the observed rotation α
We can rearrange the specific rotation formula to find the observed rotation α:
α=(α)⋅C⋅L
Substituting the values:
α=12⋅2⋅1.2
Calculating this gives:
α=12⋅2=24
α=24⋅1.2=28.8 degrees
Step 4: Determine the new concentration
When the concentration is diluted to half, the new concentration C′ becomes:
C′=22=1 g/mL
Step 5: Calculate the new specific rotation (α′)
Using the same formula for specific rotation with the new concentration:
(α′)=αC′⋅L
Substituting the values:
(α′)=28.81⋅1.2
Calculating this gives:
(α′)=28.81.2=24 units
Final Answer
The specific rotation when the concentration is halved is +24 units.
---
The specific rotation (α) is defined by the formula:
(α)=αC⋅L
where:
- α = observed rotation (in degrees)
- C = concentration (in g/mL)
- L = length of the polarimeter tube (in dm)
From the problem statement:
- The specific rotation (α) is given as +12 units.
- The concentration C is 2 g/mL.
- The length L of the polarimeter tube is 12 cm (which is 1.2 dm).
We can rearrange the specific rotation formula to find the observed rotation α:
α=(α)⋅C⋅L
Substituting the values:
α=12⋅2⋅1.2
Calculating this gives:
α=12⋅2=24
α=24⋅1.2=28.8 degrees
When the concentration is diluted to half, the new concentration C′ becomes:
C′=22=1 g/mL
Using the same formula for specific rotation with the new concentration:
(α′)=αC′⋅L
Substituting the values:
(α′)=28.81⋅1.2
Calculating this gives:
(α′)=28.81.2=24 units
The specific rotation when the concentration is halved is +24 units.
Topper's Solved these Questions
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART II SECTION (H))
4 Videos
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART II SECTION (I))
9 Videos
- STEREOISOMERISMBOOK - RESONANCE ENGLISHCHAPTER - STEREOISOMERISMEXERCISE - EXERCISE (PART II SECTION (F))
6 Videos
- SOLUTIONSBOOK - RESONANCE ENGLISHCHAPTER - SOLUTIONSEXERCISE - Advabced Level Problems (PART-2)
35 Videos
- STRUCTURAL IDENTIFICATIONBOOK - RESONANCE ENGLISHCHAPTER - STRUCTURAL IDENTIFICATIONEXERCISE - Advanced level Problems (Part-III)
12 Videos
Similar Questions
An aqueous solution containing 10gm of optically pure fructose was diluted to 500ml with water and placed in a polarimeter tube 20cm long. The measured roatation was −5.0∘. To this solution, 500ml of a solution containing 10gm of racemic fructose is added. What will be the change in specific rotation?
View SolutionThe observed rotation of 2.0 gm of a compound in 10 mL solution in
a 25 cm long polarimeter tube is +13.4∘ . The specific
rotation of compound is :
View Solution
Knowledge Check
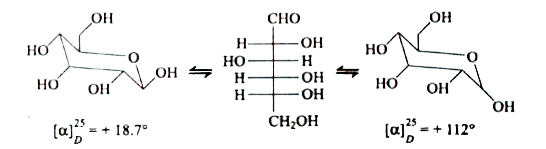
D (+) Glucose has melting point 146∘C and specific rotation [α]25D is + 112∘C. Another D(+) Glucose has melting point 150∘C and specific rotational [α]25Dis +18.7∘C. The two form have significantly different optical rotation but when an aqueous solution of either form is allowed to stand, it rotation changes. The specific rotation of one form decreases and rotation of other increases until both solution show the same value +52.7∘. The change in rotation towards an equilibrium value is called mutarotation.
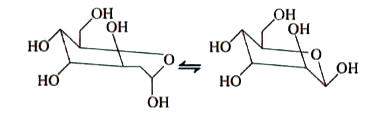
For mannose the mutarotation can be shown in brief as follow:
 Aα-formBβ-formCopen chainDNone of these
Aα-formBβ-formCopen chainDNone of theseThe observed rotation of 2.0 gm of a compound in 10 mL solution in
a 25 cm long polarimeter tube is +13.4∘ . The specific
rotation of compound is :A+30.2∘B−26.8∘C+26.8∘D+40.2∘D (+) Glucose has melting point 146∘C and specific rotation [α]25D is + 112∘C. Another D(+) Glucose has melting point 150∘C and specific rotational [α]25Dis +18.7∘C. The two form have significantly different optical rotation but when an aqueous solution of either form is allowed to stand, it rotation changes. The specific rotation of one form decreases and rotation of other increases until both solution show the same value +52.7∘. The change in rotation towards an equilibrium value is called mutarotation.
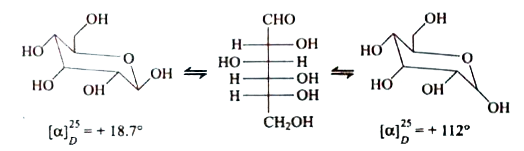
Mutarotation is characteristic feature of:AEpimerBEnantiomerCAnomerDRing chain isomer
The acid solution has a specific gravity of 1.8, when it contains 62% by weight of the acid. The solution is diluted to such an extant this its specific gravity is lowered to 1.2. what is the % by weight of the acid new solution.
View Solution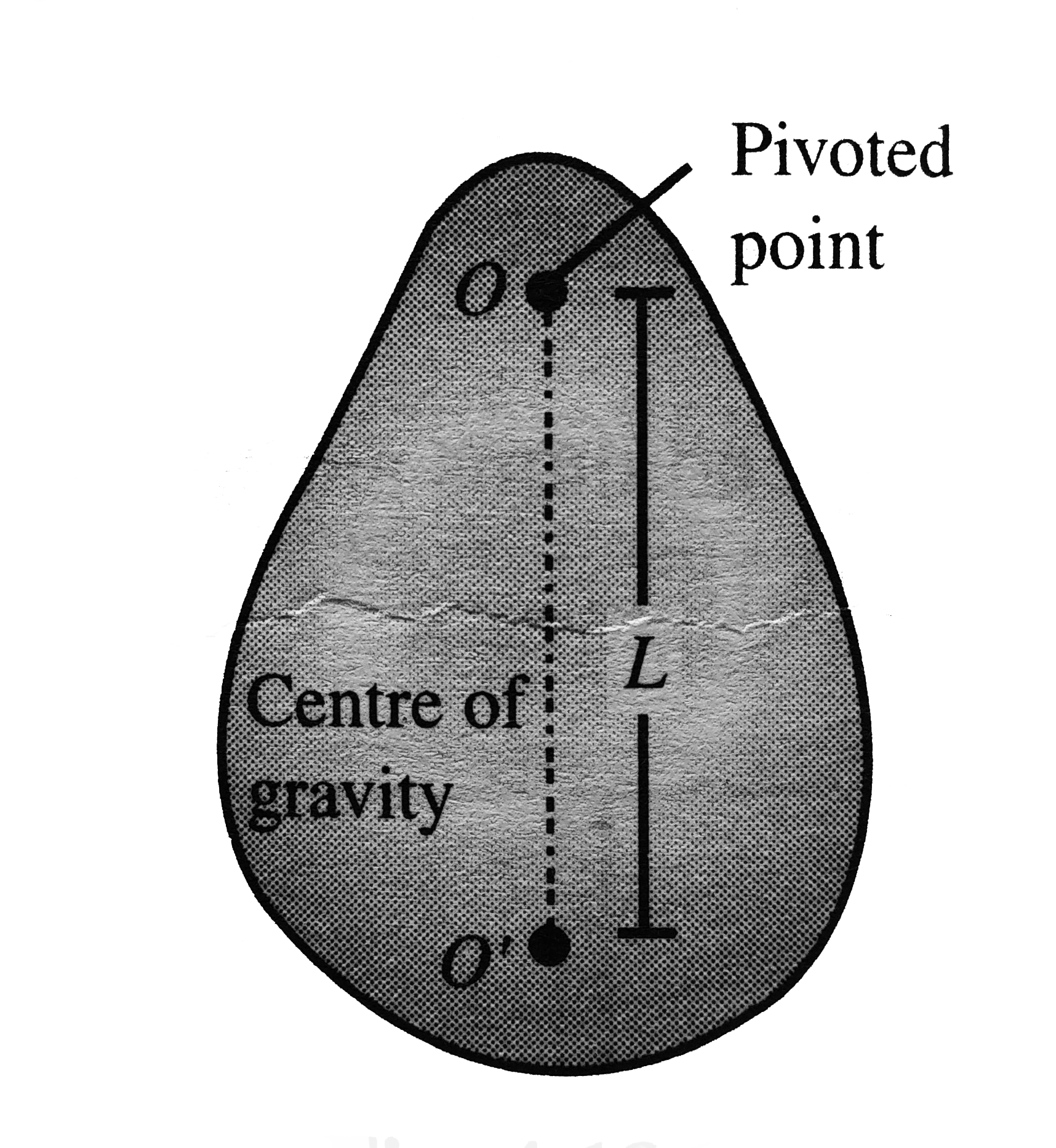
In physical pendulum, the time period for small oscillation is given by T=2π√IMgd where I is the moment of inertial of the body about an axis passing through a pivoted point O and perpendicular to the plane of oscillation and d is the separation point between centre of gravity and the pivoted point. In the physical pendulum a speacial point exists where if we concentrate the entire mass of body, the resulting simple pendulum (w.r.t. pivot point O) will have the same time period as that of physical pendulum This point is termed centre of oscillation.
T=2π√IMgd=2π√Lg Moreover, this point possesses two other important remarkable properties:
Property I: Time period of physical pendulum about the centre of oscillation (if it would be pivoted) is same as in the original case.
Property II: If an impulse is applied at the centre of oscillatioin in the plane of oscillation, the effect of this impulse at pivoted point is zero. Because of this property, this point is also known as the centre of percussion. From the given information answer the following question:
Q. A uniform rod of mass M and length L is pivoted about point O as shown in Figgt It is slightly rotated from its mean position so that it performs angular simple harmonic motion. For this physical pendulum, determine the time period oscillation.
View SolutionWhat is the observed rotation when 0.1M solutions of (R)−2 butanol is mixed with an equal volume of 0.05M solution of recemic 2−butnol and the resulting solution is taken in a cell of 5cm long tube in a polarimeter? The specific rotation of (R−2) butonal is +13.9∘
View SolutionCholesterol, when isolated from natural sources, is obtained as a single enantiomer. The observed rotation α of a 0.3 g sample of cholesterol in 5mL of chloroform solution contained in a 10 cm polarimeter tube is −0.78∘. Calculate the specific rotation of cholesterol. A sample of synthetic cholesterol was prepared consisting entirely of (+)-cholesterol. This synthetic (+)-cholesterol was mixed with some natural (-)-cholesterol. The mixture had a specific rotation [α]20D of −13∘. What fraction of the mixture was (+)-cholesterol ?
View SolutionD (+) Glucose has melting point 146∘C and specific rotation [α]25D is + 112∘C. Another D(+) Glucose has melting point 150∘C and specific rotational [α]25Dis +18.7∘C. The two form have significantly different optical rotation but when an aqueous solution of either form is allowed to stand, it rotation changes. The specific rotation of one form decreases and rotation of other increases until both solution show the same value +52.7∘. The change in rotation towards an equilibrium value is called mutarotation.
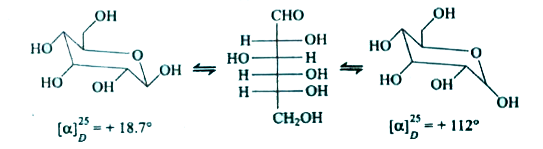
What percentage of β-D-(+) glucopyranose found at equilibrium in the aqueous solution?
View Solution
