For making graph of equations |y|=|f(|x|)| through y=f(x) which order of step is right among the following order of
Step I:y=f(|x|) (replace x by |x|)
Step II:y=|f(x)| (take modulus of R.H.S)
StepIII : |y|=f(x)(replaceyby|y|)(A) I, II, III(B) II, I, III(C) III, II, I(D) III, I, II
I, II, III
II, I, III
III, II, I
III, I, II
The correct Answer is:B
Step by step video & image solution for For making graph of equations |y|=|f(|x|)| through y=f(x) which order of step is right among the following order of Step I : y=f(|x|) (replace x by |x|) Step II : y=|f(x)| (take modulus of R.H.S) Step III : |y|=f(x) (replace y by |y|) (A) I, II, III (B) II, I, III (C) III, II, I (D) III, I, II by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Which of the following relations are even?
I. y=2
II. f(x)=x
III. x2+y2=1AOnly IBOnly I and IICOnly II and IIIDonly I and IIIWhich of the following relations are odd?
I. y=2
II. y=x
III. x2+y2=1Aonly IIBonly I and IIIConly II and IIIDI,II and IIIWhich of the following lins are asymptotes of the graph of y=xx+1?
I. x=1
II. x=−1
III. y=1AI onlyBII onlyCIII onlyDII and III
Sketch the origin in which the points satisfying the following inequalities lie.
(i)|x+y|<2 (ii) |2x−y|>3 (iii) |x|>|y|
View SolutionWrite four solutions for each of the following equations:
(i) 2x+y=7
(ii) πx+y=9
(iii) x=4y
View SolutionThe graph of the function y=f(x) is as shown in the figure.

Then draw the graphs of
(i) |y|=sgn(f(x)) (ii) |y|=|f(x∣)|
(iii) y=xsgn(f(x))
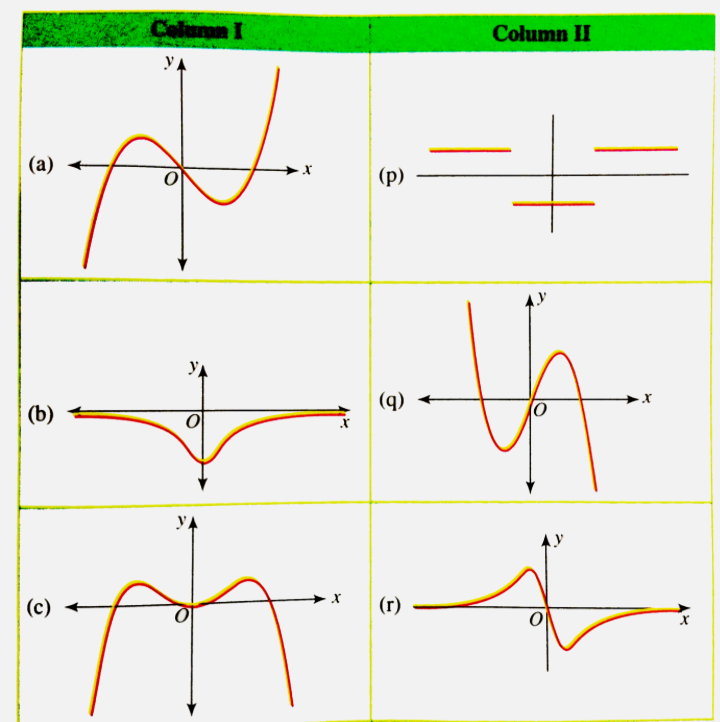
View SolutionMatch the graph of y = f(x) in Column I with the corresponding graph of y = f'(x) in Column II.

View SolutionDraw the graph of each of the following equations:
(i) y=3 (ii) y+5=0 (iii) x=4 (iv) x=6=0
View Solution

