Let the co-efficients of xn In (1+x)2nand(1+x)2n−1 be P & Qrespectively, then (P+QQ)5=
9
27
81
None of these
The correct Answer is:A
Step by step video & image solution for Let the co-efficients of x^n In (1+x)^(2n) and (1+x)^(2n-1) be P & Qrespectively, then ((P+Q)/Q)^5= by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
The coefficients of xp and xq(p,q∈N) in the expansion of (1+x)p+q are
AequalBequal with opposite signCreciprocal of each otherDNone of theseIf P be the sum of odd terms and Q be the sum of even terms in the expansion of (x+a)n, then (x+a)2n+(x−a)2n is
(i) P2−Q2
(ii) P2+Q2
(iii) 2(P2+Q2)
(iv) 4PQAP2−Q2BP2+Q2C2(P2+Q2)D4PQ
cos−1(1−x2n1+x2n)
View SolutionIf (n)C0,(n)C1,(n)C2,....,(n)Cn, denote the binomial coefficients in the expansion of (1+x)nandp+q=1 n∑r=0r2 nCrprqn−r= .
View SolutionFind n if :
2n+1Pn−1:2n−1Pn=3:5
View SolutionIf pandq are positive, then prove that the coefficients of xpandxq in the expansion of (1+x)p+q will be equal.
View SolutionIn the given figure graph of :
y=p(x)=xn+a1xn−1+a2xn−2+…..+an is given.
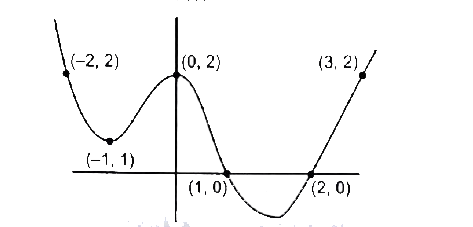
The product of all imaginary roots of p(x)=0 is:
View SolutionIf xp occurs in the expansion of (x2+1x)2n, prove that its coefficient is (2n)![13(4n−p)!][13(2n+p)!]
View Solution