There are several tea cups in the kitchen, some with handle and the others without handles. The number of ways of selecting two cups without a handle and three with a handle is exactly 1200. What is the maximum possible number of cups in the kitchen?
The correct Answer is:29
To solve the problem, we need to determine the maximum number of tea cups in the kitchen, given the conditions regarding the selection of cups with and without handles.
1. Define Variables:
Let x be the number of cups without handles and y be the number of cups with handles.
2. Set Up the Equation:
The number of ways to select 2 cups without handles is given by (x2) and the number of ways to select 3 cups with handles is given by (y3). According to the problem, we have:
(x2)⋅(y3)=1200
3. Express the Combinations:
The combinations can be expressed as:
(x2)=x(x−1)2and(y3)=y(y−1)(y−2)6
Substituting these into the equation gives:
x(x−1)2⋅y(y−1)(y−2)6=1200
Simplifying this, we get:
x(x−1)⋅y(y−1)(y−2)12=1200
Multiplying both sides by 12 results in:
x(x−1)⋅y(y−1)(y−2)=14400
4. Factorization:
We need to find integer values for x and y such that the product x(x−1)⋅y(y−1)(y−2)=14400.
5. Finding Possible Values:
We can factor 14400 to find suitable pairs of x(x−1) and y(y−1)(y−2). The prime factorization of 14400 is:
14400=26⋅32⋅52
We will check different values for y and calculate y(y−1)(y−2) to find corresponding x(x−1).
6. Testing Values for y:
- For y=4:
y(y−1)(y−2)=4⋅3⋅2=24
Then,
x(x−1)=1440024=600
Solving x(x−1)=600 gives x=25 (since 25⋅24=600).
- For y=5:
y(y−1)(y−2)=5⋅4⋅3=60
Then,
x(x−1)=1440060=240
Solving x(x−1)=240 gives x=16 (since 16⋅15=240).
- For y=6:
y(y−1)(y−2)=6⋅5⋅4=120
Then,
x(x−1)=14400120=120
Solving x(x−1)=120 gives x=11 (since 11⋅10=110).
- For y=10:
y(y−1)(y−2)=10⋅9⋅8=720
Then,
x(x−1)=14400720=20
Solving x(x−1)=20 gives x=6 (since 6⋅5=30).
7. Finding Maximum:
The combinations we found are:
- (x,y)=(25,4) → Total = 29
- (x,y)=(16,5) → Total = 21
- (x,y)=(11,6) → Total = 17
- (x,y)=(6,10) → Total = 16
The maximum total is when x=25 and y=4, which gives:
Maximum number of cups=25+4=29
Final Answer:
The maximum possible number of cups in the kitchen is 29.
Let x be the number of cups without handles and y be the number of cups with handles.
The number of ways to select 2 cups without handles is given by (x2) and the number of ways to select 3 cups with handles is given by (y3). According to the problem, we have:
(x2)⋅(y3)=1200
The combinations can be expressed as:
(x2)=x(x−1)2and(y3)=y(y−1)(y−2)6
Substituting these into the equation gives:
x(x−1)2⋅y(y−1)(y−2)6=1200
Simplifying this, we get:
x(x−1)⋅y(y−1)(y−2)12=1200
Multiplying both sides by 12 results in:
x(x−1)⋅y(y−1)(y−2)=14400
We need to find integer values for x and y such that the product x(x−1)⋅y(y−1)(y−2)=14400.
We can factor 14400 to find suitable pairs of x(x−1) and y(y−1)(y−2). The prime factorization of 14400 is:
14400=26⋅32⋅52
We will check different values for y and calculate y(y−1)(y−2) to find corresponding x(x−1).
- For y=4:
y(y−1)(y−2)=4⋅3⋅2=24
Then,
x(x−1)=1440024=600
Solving x(x−1)=600 gives x=25 (since 25⋅24=600).
- For y=5:
y(y−1)(y−2)=5⋅4⋅3=60
Then,
x(x−1)=1440060=240
Solving x(x−1)=240 gives x=16 (since 16⋅15=240).
- For y=6:
y(y−1)(y−2)=6⋅5⋅4=120
Then,
x(x−1)=14400120=120
Solving x(x−1)=120 gives x=11 (since 11⋅10=110).
- For y=10:
y(y−1)(y−2)=10⋅9⋅8=720
Then,
x(x−1)=14400720=20
Solving x(x−1)=20 gives x=6 (since 6⋅5=30).
7. Finding Maximum:
The combinations we found are:
- (x,y)=(25,4) → Total = 29
- (x,y)=(16,5) → Total = 21
- (x,y)=(11,6) → Total = 17
- (x,y)=(6,10) → Total = 16
Maximum number of cups=25+4=29
The maximum possible number of cups in the kitchen is 29.
Topper's Solved these Questions
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-2 (Part-II: Previously Asked Question of RMO)
5 Videos
- COMBINATORICSBOOK - RESONANCE ENGLISHCHAPTER - COMBINATORICSEXERCISE - Exercise-1 (Part-II RMO)
11 Videos
- APPLICATION OF DERIVATIVESBOOK - RESONANCE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - High Level Problems (HLP)
35 Videos
- DEFINITE INTEGRATION & ITS APPLICATION BOOK - RESONANCE ENGLISHCHAPTER - DEFINITE INTEGRATION & ITS APPLICATION EXERCISE - High Level Problem
26 Videos
Similar Questions
If n objects are arrange in a row, then the number of ways of selecting three of these objects so that no two of them are next to each other is
View SolutionA drawer contains a mixture of red socks and blue socks, at most 17 in all. It so happens that when two socks are selected randomly without replacement, there is a probability of exactly 1/2 that both are red or blue. The largest possible number of red socks in the drawer that is consistent with this data is _______.
View Solution
In the figure above, a rectangular container with the dimensions 10 inches by 15 inches by 20 inches is to be filled with water, using a cylindrical cup whose radius is 2 inches and whose height is 5 inches. What is the maximum number of full cups of water that can be placed into the container without the water overflowing the container?
View SolutionIn the next world cup of cricket there will be 12 teams, divided equally in two groups. Teams of each group will play a match against each other. From each group 3 top teams will qualify for the next round.In this round each team will play against other once. Each of the four top teams of this round will play amatch against the other three. Two top teams of this round will go to the final round, where they will playthe best of three matches. The minimum number of matches in the next world cup will be
View SolutionThere are 10 different books in a shelf. The number of ways in which three books can be selected so that exactly two of them are consecutive is
View SolutionA salad dressing requires oil, vineger, and water in the ratio 2:1:3. If Oliver has 1 cup of oil, 1/3 cup of vinegar, and 2 cups of water, what is the maximum number of cups of dressing that can mix?
View Solution20 persons are sitting in a particular arrangement around a circular table. Three persons are to be selected for leaders. The number of ways of selection of three persons such that no two were sitting adjacent to each other is a. 600 b. 900 c. 800 d. none of these
View SolutionIf n objects are arrange in a row, then the number of ways of selecting three of these objects so that no two of them are next to each other is a. n−2C3 b. n−3C2 c. n−3C3 d. none of these
View SolutionA small firm manufactures necklaces and bracelets. The total number of necklaces and bracelets that it can handle per day is at most 24. It takes 1 hour to make a bracelet and half an hour to make a necklace. The maximum number of hours available per day is 16. If the profit on a necklace is Rs 100 and that on a bracelet is Rs 300, how many of each should be produced daily to maximize the profit?
View SolutionA manufacturer manufactures two types of tea-cups, A and B. Three machines are needed for manufacturing the tea cups. The time in minutes required for manufacturing each cup on the machines is given below:
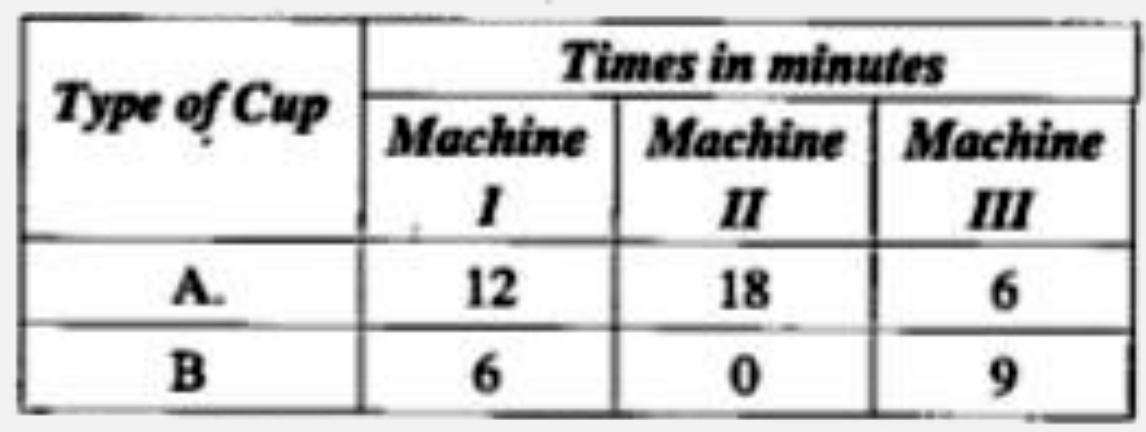
Each machine is available for a maximum of six hours per day. If the profit on each cup of type A is Rs 1.50and that'on each cup of type B is Rs 1.00, find the number of cups of each type that should be manufactured in a day to get maximumprofit.
View Solution
