Starting with ? r= , Show that the speed of electron in nth orbit varies inversely to principal quantum number.
To show that the speed of an electron in the nth orbit varies inversely with the principal quantum number n, we start with the given formula for the radius of the orbit:
r=ϵ0h2n2πmZe2
Step 1: Angular Momentum Relation
According to Bohr's model, the angular momentum L of the electron is quantized and given by:
L=mvr=nh2π
Step 2: Squaring the Angular Momentum Equation
Squaring both sides of the angular momentum equation gives:
(mvr)2=(nh2π)2
This can be expanded to:
m2v2r2=n2h24π2
Step 3: Isolating v2
We can isolate v2 from the equation:
v2=n2h24π2mr
Step 4: Substituting for r
Now, substitute the expression for r from the first step into the equation for v2:
v2=n2h24π2m(ϵ0h2n2πmZe2)
Step 5: Simplifying the Expression
This simplifies to:
v2=n2h2⋅πmZe24π2mϵ0h2n2
Cancelling n2 and h2:
v2=Ze24ϵ0π
Step 6: Taking the Square Root
Taking the square root gives us the speed v:
v=√Ze24ϵ0π
Step 7: Establishing the Inverse Relationship
Notice that the expression for v does not depend on n. However, we need to show that speed varies inversely with n.
From our earlier expression for v2:
v2∝1n2
Thus, taking the square root:
v∝1n
Conclusion
Therefore, we have shown that the speed of the electron in the nth orbit varies inversely with the principal quantum number n:
v∝1n
According to Bohr's model, the angular momentum L of the electron is quantized and given by:
Squaring both sides of the angular momentum equation gives:
We can isolate v2 from the equation:
Now, substitute the expression for r from the first step into the equation for v2:
This simplifies to:
Taking the square root gives us the speed v:
Notice that the expression for v does not depend on n. However, we need to show that speed varies inversely with n.
Therefore, we have shown that the speed of the electron in the nth orbit varies inversely with the principal quantum number n:
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Structure of Atoms and Nuclei ( Short Answer II (SA2) ( 3 MARKS Each ) )
7 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Structure of Atoms and Nuclei (Long Answer ( LA) ( 4 marks Each) )
3 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Structure of Atoms and Nuclei (Very Short Answer (VSA) ( 1 MARK Each ) )
9 Videos
- MULTIPLE CHOICE QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - MULTIPLE CHOICE QUESTIONSEXERCISE - Communication Systems
6 Videos
- SHORT ANSWER QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - SHORT ANSWER QUESTIONSEXERCISE - Assignments
3 Videos
Similar Questions
Show that the radius of the orbit in hydrogen atom varies as n2, where n is the principal quantum number of the atom.
View SolutionAccording to Bohr's theory of the hydrogen atom, the speed vn of the electron in a stable orbit is related to the principal quantum number n as (C is a constant) :
View Solution
Knowledge Check
Speed (Vn) of electron in nth orbit versus principal quantum number (n) graphs is
A B
B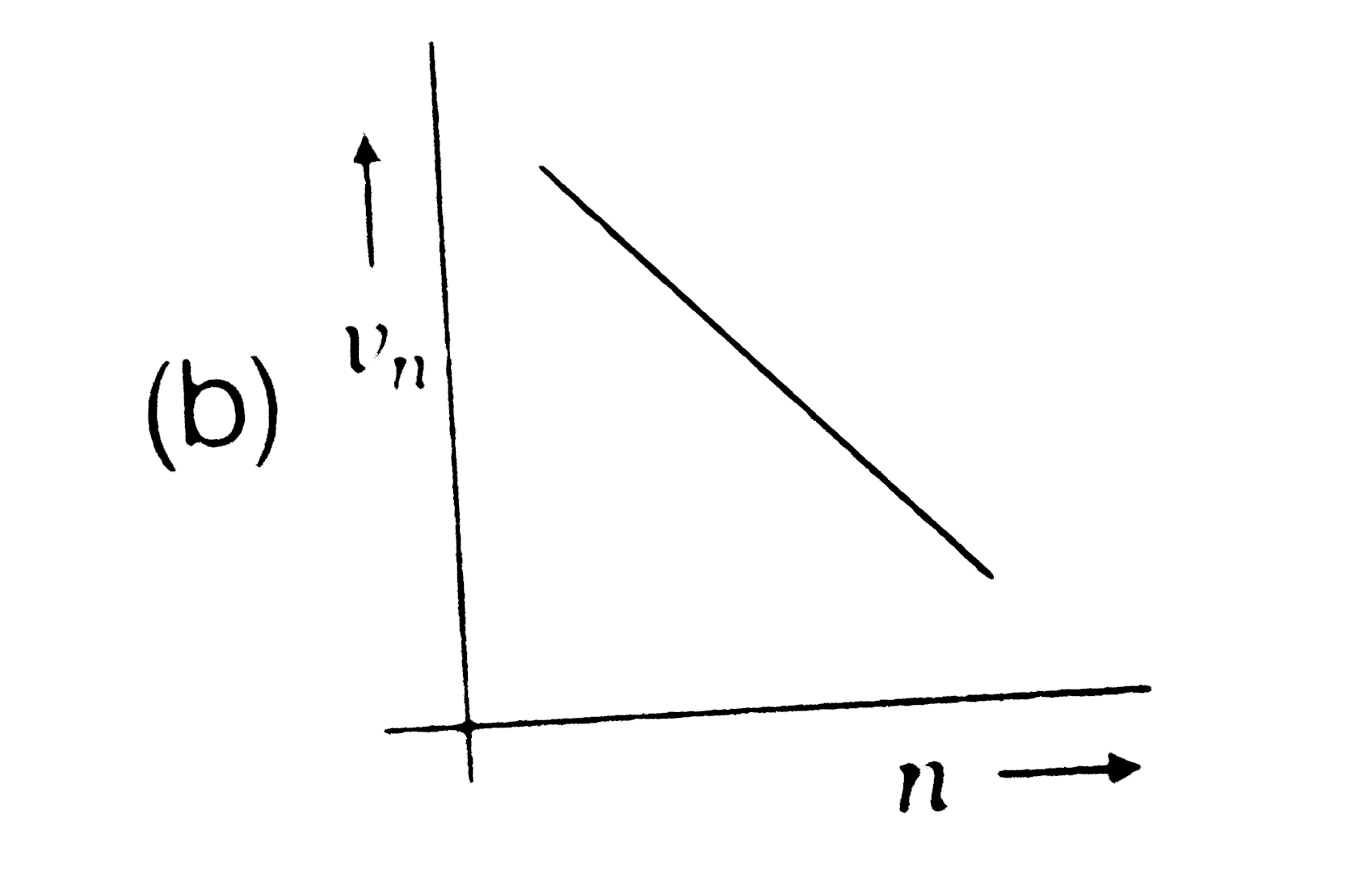 C
C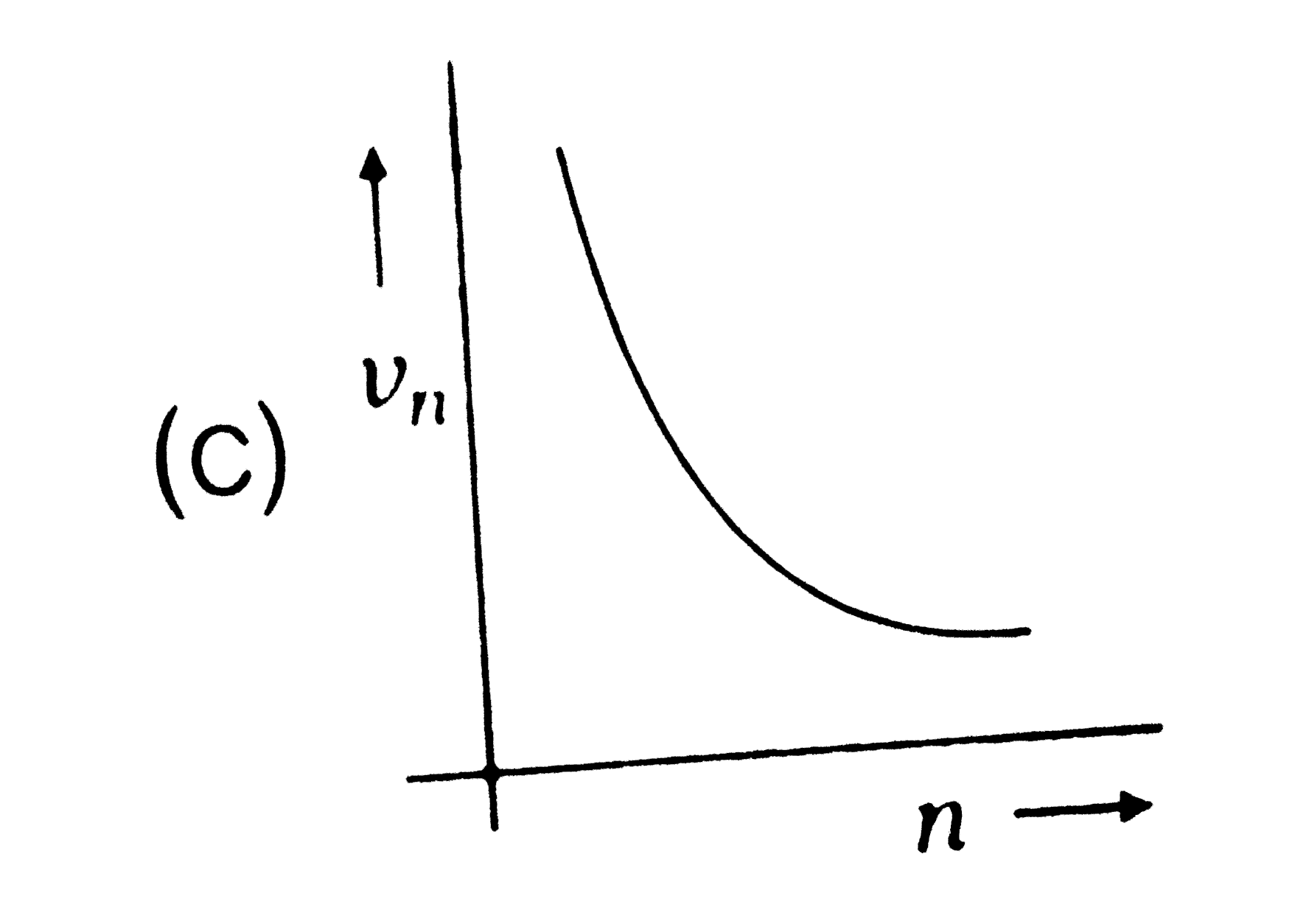 D
D
the number of electrons accommodated in an orbital with principal quantum number 3 is
A2B6C8D18The total number of orbitals in a shell with principal quantum number n is :
A2nB2n2Cn2Dn+1
Show graphically the nature of variation of radius of orbit with the principal quantum number.
View SolutionThe total number of orbitals in a shell having principal quantum n is
View SolutionAssertion (A) : In a hydrogen atom the radius of nth orbit is directly proportional to the quantum number n.
Reason (R) : The speed of electron in nth orbitis inversely proportional to the quantum number.
View SolutionSpeed of a revolving electron around the nucleus varies with principal quantum number n as :
View SolutionThe maximum number of electrons in the shell with principal quantum number n is equal to
View Solution
