Show that the radius of the orbit in hydrogen atom varies as n2, where n is the principal quantum number of the atom.
To show that the radius of the orbit in a hydrogen atom varies as n2, where n is the principal quantum number, we can use the Bohr model of the hydrogen atom. Here is a step-by-step solution:
Step 1: Understand the Forces Acting on the Electron
In a hydrogen atom, the electron is attracted to the nucleus (proton) by the electrostatic force. According to Coulomb's law, the electrostatic force F between the electron and the proton is given by:
F=k⋅e2r2
where:
- k is Coulomb's constant,
- e is the charge of the electron,
- r is the radius of the orbit.
Step 2: Equate Electrostatic Force to Centripetal Force
For an electron moving in a circular orbit, the centripetal force required to keep it in that orbit is provided by the electrostatic force. Thus, we can write:
k⋅e2r2=mv2r
where:
- m is the mass of the electron,
- v is the velocity of the electron.
Step 3: Rearranging the Equation
Rearranging the above equation gives:
k⋅e2=mv2⋅r
This equation relates the radius r to the velocity v.
Step 4: Angular Momentum Quantization
According to Bohr's postulate, the angular momentum L of the electron in the nth orbit is quantized and is given by:
L=mvr=nh2π
where:
- h is Planck's constant,
- n is the principal quantum number.
Step 5: Solve for Velocity
From the angular momentum equation, we can express the velocity v as:
v=nh2πmr
Step 6: Substitute Velocity into the Force Equation
Substituting this expression for v back into the centripetal force equation:
k⋅e2=m(nh2πmr)2⋅r
Simplifying this gives:
k⋅e2=n2h24π2mr
Step 7: Solve for Radius r
Rearranging the equation to solve for r:
r=n2h24π2mke2
This shows that r is proportional to n2:
r∝n2
Conclusion
Thus, we have shown that the radius of the orbit in a hydrogen atom varies as n2.
---
In a hydrogen atom, the electron is attracted to the nucleus (proton) by the electrostatic force. According to Coulomb's law, the electrostatic force F between the electron and the proton is given by:
F=k⋅e2r2
where:
- k is Coulomb's constant,
- e is the charge of the electron,
- r is the radius of the orbit.
For an electron moving in a circular orbit, the centripetal force required to keep it in that orbit is provided by the electrostatic force. Thus, we can write:
k⋅e2r2=mv2r
where:
- m is the mass of the electron,
- v is the velocity of the electron.
Rearranging the above equation gives:
k⋅e2=mv2⋅r
This equation relates the radius r to the velocity v.
According to Bohr's postulate, the angular momentum L of the electron in the nth orbit is quantized and is given by:
L=mvr=nh2π
where:
- h is Planck's constant,
- n is the principal quantum number.
From the angular momentum equation, we can express the velocity v as:
v=nh2πmr
Substituting this expression for v back into the centripetal force equation:
k⋅e2=m(nh2πmr)2⋅r
Simplifying this gives:
k⋅e2=n2h24π2mr
Rearranging the equation to solve for r:
r=n2h24π2mke2
This shows that r is proportional to n2:
r∝n2
Thus, we have shown that the radius of the orbit in a hydrogen atom varies as n2.
Topper's Solved these Questions
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)EXERCISE - SECTION C15videos
CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)EXERCISE - SECTION E6videos
CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)EXERCISE - SECTION E6videos
CBSE EXAMINATION PAPER, DELHI REGION - 2015 (CODE NO. 55/1/1/D)
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - CBSE Examination Paper Delhi–2014EXERCISE - SET-III (Questions Uncommon to set-I and II)9videos
CBSE Examination Paper Delhi–2014
- BOOK - CBSE COMPLEMENTARY MATERIALCHAPTER - DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEIEXERCISE - Long Answer Question22videos
DUAL NATURE OF MATTER AND RADIATION & ATOMS AND NUCLEI
Similar Questions
Knowledge Check
- Question 1 - Select One
The force acting on the electron in a hydrogen atom depends on the principal quantum number as
AF∝n2BF∝1n2CF∝n4DF∝1n4 - Question 2 - Select One
The radius of the hydrogen atom in its ground state is 5.3×10−11 m. The principal quantum number of the final state of the atom is
A2B3C4D16 - Question 3 - Select One
Which of the following curves may represent the speed of the electron in a hydrogen atom as a function of the principal quantum number n ?
A B
B C
C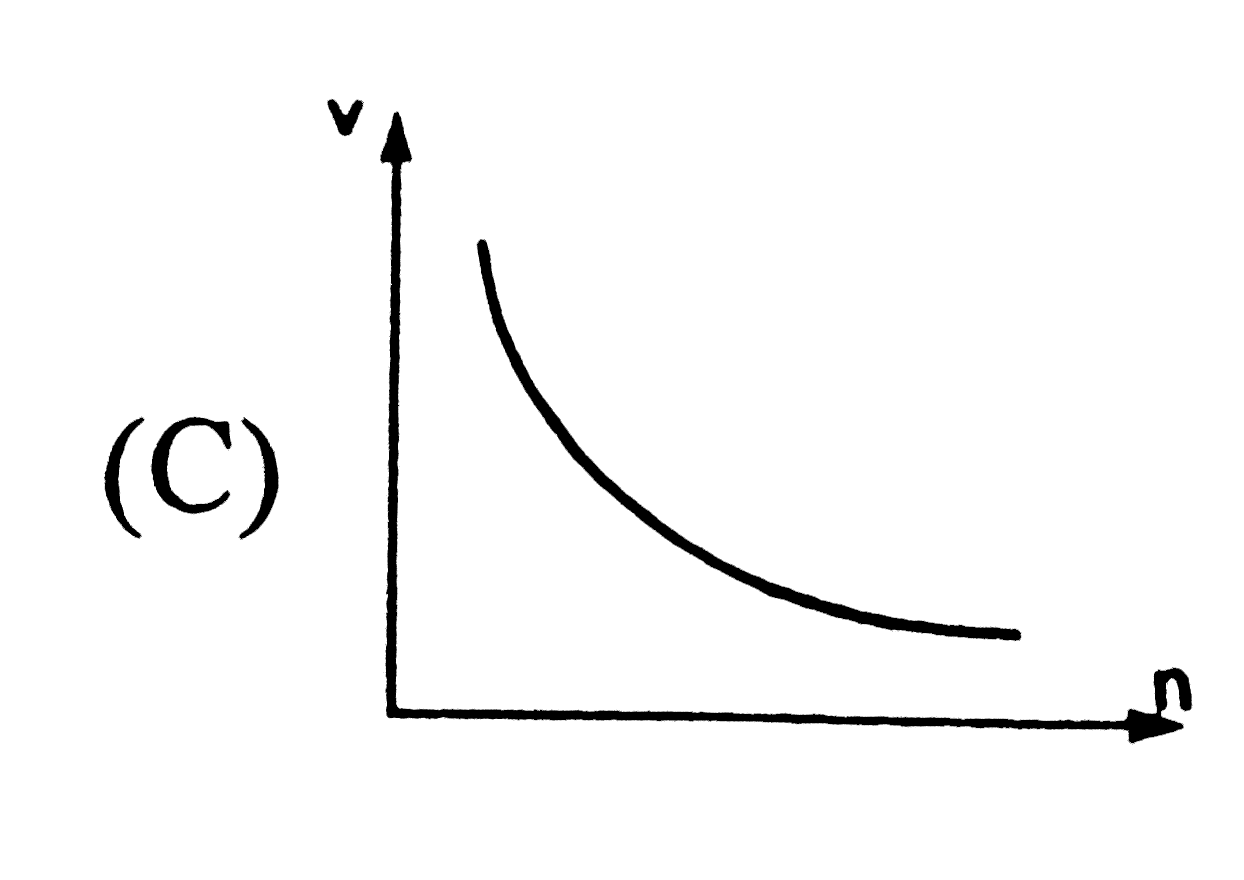 D
D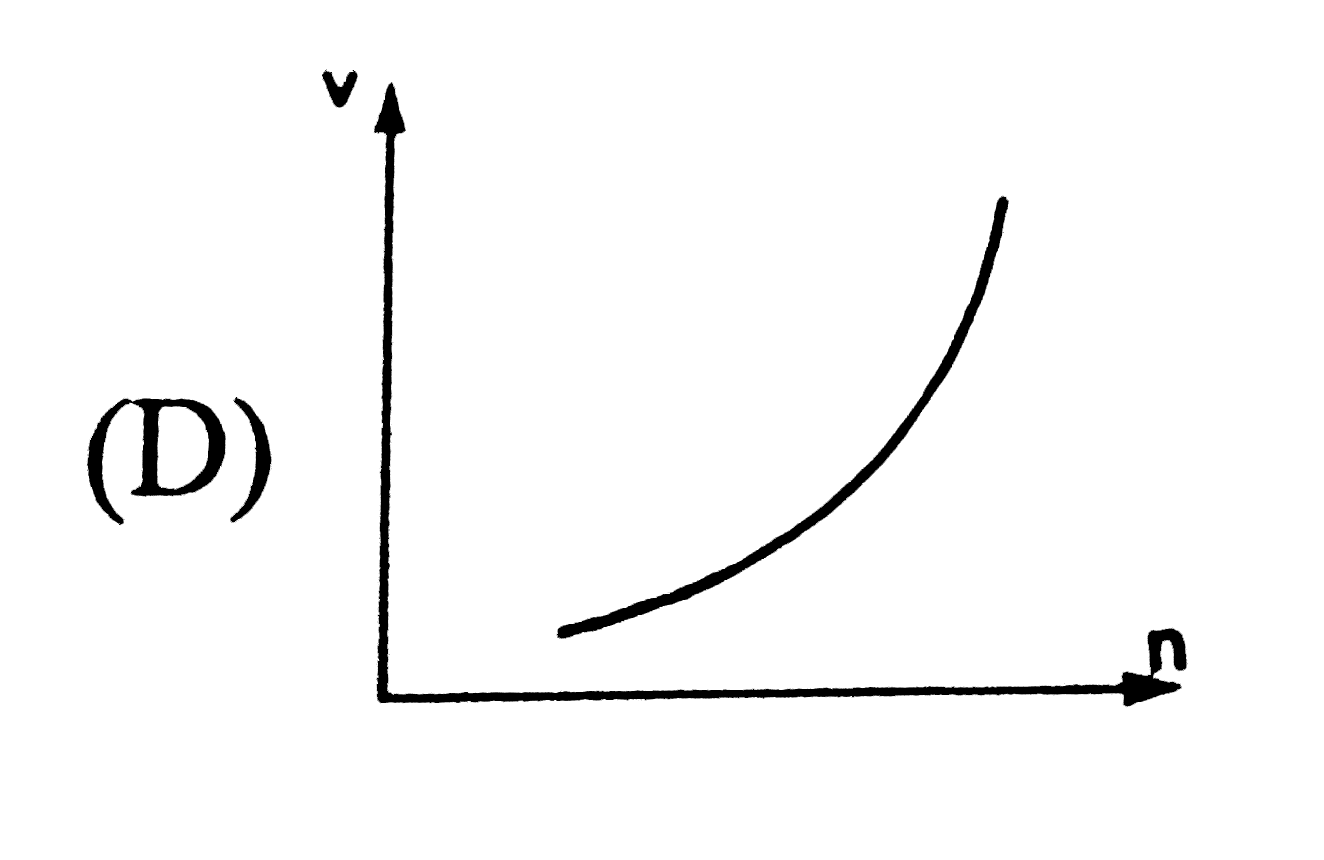
The principal quantum number determines ……….of the atom
View SolutionUsing the expression for the radius of orbit for Hydrogen atom , show that the linear speed varies inversely to principal quantum number n the angular speed varies inversely to the cube of principal quantum number n.
View SolutionStarting with ? r= εoh2n2πmZe2, Show that the speed of electron in nth orbit varies inversely to principal quantum number.
View SolutionThe energy of an excited hydrogen atom is -3.4eV. The principal quantum number of the orbit is
View SolutionThe electron in hydrogen atom makes a transition n1→n2 where n1 and n2 are the principal quantum number of two states. Assuming the Bohr model to be valid, the time period of the electron in the initial state is eight times that in the final state. The possible value of n1 and n2 are:
View Solution

