If there are n jobs and m machines, then there will be ......….sequence of doing jobs.
mn
m(n!)
nm
(n!)m
The correct Answer is:D
To solve the problem of determining the number of sequences of doing jobs when there are n jobs and m machines, we can follow these steps:
1. Understand the Problem: We have n jobs and m machines. We need to find out how many different sequences there are for completing these jobs across the machines.
Hint: Think about how each job can be assigned to any of the machines.
2. Identify the Formula: The total number of sequences of doing jobs can be calculated using the formula:
Total sequences=(n!)m
where n! (n factorial) represents the number of ways to arrange n jobs, and raising it to the power of m accounts for the m machines.
Hint: Recall that n! is the product of all positive integers up to n.
3. Substitute the Variables: In our case, we replace n with the number of jobs and m with the number of machines:
Total sequences=(n!)m
Hint: Make sure to keep track of the factorial notation.
4. Final Expression: Therefore, the final expression for the total number of sequences of doing jobs when there are n jobs and m machines is:
(n!)m
Hint: This expression indicates that for each machine, the jobs can be arranged in n! different ways.
Conclusion:
If there are n jobs and m machines, then there will be (n!)m sequences of doing jobs.
Total sequences=(n!)m
where n! (n factorial) represents the number of ways to arrange n jobs, and raising it to the power of m accounts for the m machines.
Total sequences=(n!)m
(n!)m
If there are n jobs and m machines, then there will be (n!)m sequences of doing jobs.
Topper's Solved these Questions
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II ASSIGNMENT PROBLEMS AND SEQUENCING (II. Fill in the blanks)
12 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II ASSIGNMENT PROBLEMS AND SEQUENCING (III. State whether each of the following is true or false.)
12 Videos
- QUESTION BANK 2021BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - QUESTION BANK 2021EXERCISE - Part II LINEAR PROGRAMMING PROBLEMS (E. Activities)
3 Videos
- PROBABILITY DISTRIBUTIONBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - MULTIPLE CHOICE QUESTIONS
9 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - MULTIPLE CHOICE QUESTIONS
8 Videos
Similar Questions
The Hungarian method is used to assign n jobs on 2 machines to get the optimal sequence. (True/False)
View SolutionFive jobs must pass through a lathe and a surface grinder, in that order. The processing time in hours are shown below. Determine the optimal sequence of the jobs. Also, find the idle time of each machine:
View Solution
Knowledge Check
If x can finish a job in 4 hours and y can finish the same job in 8 hours independently, then they together will finish the job in:
A160 minutesB150 minutesC140 minutesD120 minutesA takes three times as long as B and C together to do a job. B takes four times as long as A and C together to do the work. If all the three, working together can complete the job in 24 days, then the number of days, A alone will take to finish the job is
A100B96C95D90If 10 people can do a job in 20 days, then 20 people with twice the efficiency can do the same job in
A5 daysB10 daysC20 daysD40 days
Solve the following problem of sequencing for minimizing the total elapsed time and idle time for both the machines.

The optimal sequence of the jobs as follows:

Total elapsed time is obtained as follows:
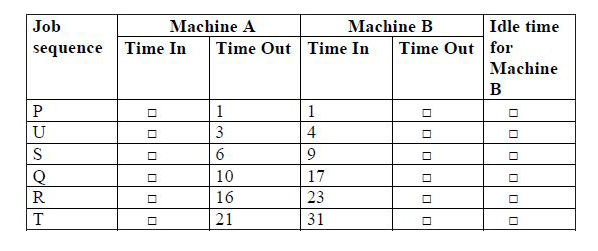
Total elapsed time T=□ minutes
Idle time for Machine A=T−□=□ minutes
Idle time for Machine B=□
View SolutionFind the sequence that minimizes the total elapsed time to complete the following jobs. Each job is processed in the order AB:

Determine the sequence for the jobs so as to minimize the processing time. Find the total elapsed time and the idle times for both the machines.
View SolutionThe idle time for a machine is the time when machine is available but is not waiting for any job to be processed. (True/False)
View SolutionWhat job does the pupil of the eye do ?
View SolutionA company has a job to prepare certain number cans and there are three machines A, B and C for this job. A can complete the job in 3 days, B can complete the job in 4 days, and C can complete the job in 6 days. How many days will the company take to complete the job if all the machines are used simultaneously?
View Solution
