Find the foot of the perpendicular drawn from the point (5,7,3) to the line x−153=y−298=z−5−5. Find the length of the perpendicular.Solution in Odia
Step by step video & image solution for Find the foot of the perpendicular drawn from the point (5,7,3) to the line frac[x-15][3]=frac[y-29][8]=frac[z-5][-5]. Find the length of the perpendicular. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A is a square matrix of order 3. write the value n, |2A|=n|A|.
View SolutionLet f(x)=2lnx and g(x)=lnx2 .Do you think f=g ? Justify
View SolutionFind the foot and hence the lengh of perpendicular form (5,7,3) to the line x−153=y−298=z−5−5. Find also the equation of the perpendicular.
View Solutionबिंदु (5,7,3) से रेखा x−153=y−298=z−5−5 पर खींचे गए लम्ब का पाद तथा लम्बाई ज्ञात करें| लम्ब का समीकरण भी निकाले|
View SolutionFind x such that:
(i) −15=8x
(ii) 7−3=x6
(iii) 35=x−25
(iv) 136=−65x
(v) 16x=−4
(vi) −48x=2
View Solutionকলনবিদ্যার সাহায্যে দেখাও যে, x225+y29=1 এই উপবৃত্তের (5√2,3√2) বিন্দুতে অঙ্কিত অভিলম্বের সমীকরণ 5x−3y=8√2 এই সরলরেখা।
View Solutionநேர்க்கோடுகள் x−32=y+54=z−1−13 மற்றும் x+13=y−45=z+22என்பது
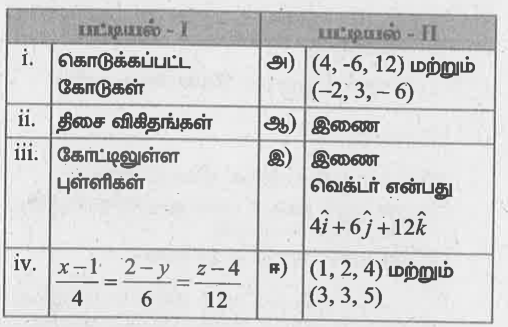
View Solutionபொருத்துக: கோடுகளுக்கு x−14=2−y6=z−412,x−3−2=y−33=5−z6
View SolutionFind d.r. of the line 4−x2=y6=1−z3
View SolutionDirection cosines of the line parallel to line x−52=y+3−3=z−56
View SolutionProve that the lines x+32=y+53=z−7−3 and x+14=y+15=z+1−1 are coplanar. Find the equation of plane containing them.
View SolutionFind the shortest distance between the lines frac[x][2]=frac[y][-3]=frac[z][1] and frac[x-2][3]=frac[y-1][-5]=frac[z+2][2] .
View SolutionIf x=−38 then find the value of 2x+5,x + 38, 5 - (-x).
View Solutionबिंदु (5,7,3) से रेखा x−153=y−298=5−z5 पर डाले गए लम्ब की लम्बाई तथा पाद के निर्देशांक ज्ञात कीजिए और उस समतल का समीकरण भी ज्ञात कीजिए जिसमे दी गई रेखा व लम्ब स्थित है।
View SolutionFind the foot of the perpendicular drawn from the point (5,7,3) to the line x−153=y−298=z−5−5. Find the length of the perpendicular.
View SolutionFind the distance of the point (2,3,4) from the plane 3x+2y+2z+5=0 measured parallel to the line frac[x+3][3]=frac[y-2][6]=frac[z][2] .
View Solution
