The straight line x+2y=1 meets the coordinate axes at A and B. A circle is drawn through A, B and the origin. Then the sum of perpendicular distances from A and B on the tangent to the circle at the origin is
2√5
√52
4√5
√54
The correct Answer is:B
A(1,0), B(0,12) and O(0,0)
AB is diameter of the circle so equation is (x-1)(x-0)+(y-0)(y−12)=0
⇒x2+y2−x−12y=0
Equation of tangent at O(0,0) is given by T=0 ⇒ 2x+y=0
Sum of ⊥ distances from A and B to tangents is =2√5+12√5=52√5=√52
Topper's Solved these Questions
Similar Questions
A line 2x+y=1 intersect co-ordinate axis at points A and B. A circle is drawn passing through origin and point A & B. If perpendicular from point A and B are drawn on tangent to the circle at origin then sum of perpendicular distance is (A) 5√2 (B) √52 (C) √54 (D) 52
View SolutionA line meets the coordinate axes at A and B . A circle is circumscribed about the triangle OAB. If d1andd2 are distances of the tangents to the circle at the origin O from the points AandB , respectively, then the diameter of the circle is (a)2d1+d22 (b) d1+2d22 (c)d1+d2 (d) d1d2d1+d2
View SolutionThe straight line xa+yb=1 cuts the coordinate axes at A and B . Find the equation of the circle passing through O(0,0),AandB.
View SolutionFind the locus of the feet of the perpendiculars drawn from the point (b, 0) on tangents to the circle x2+y2=a2
View SolutionA line meets the co-ordinates axes at A(a, 0) and B(0, b) A circle is circumscribed about the triangle OAB. If the distance of the points A and B from the tangent at origin to the circle are 3 and 4 repectively, then the value of a2+b2+1 is
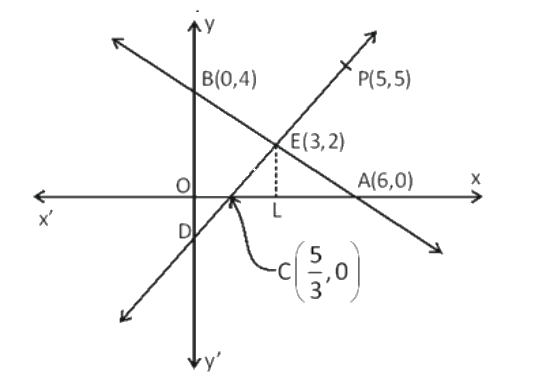
View SolutionThe line 2x+3y=12 meets the coordinates axes at A and B respectively. The line through (5, 5) perpendicular to AB meets the coordinate axes and the line AB at C, D and E respectively. If O is the origin, then the area (in sq. units) of the figure OCEB is equal to
View SolutionThe tangent at any point P on the circle x2+y2=4 meets the coordinate axes at AandB . Then find the locus of the midpoint of AB.
View SolutionThe line 3x+6y=k intersects the curve 2x2+3y2=1 at points AandB . The circle on AB as diameter passes through the origin. Then the value of k2 is__________
View SolutionA variable chord is drawn through the origin to the circle x2+y2−2ax=0 . Find the locus of the center of the circle drawn on this chord as diameter.
View SolutionThe tangent at any point to the circle x2+y2=r2 meets the coordinate axes at A and B. If the lines drawn parallel to axes through A and B meet at P then locus of P is
View Solution