A square is inscribed in the circle with its sides parallel to the coordinate axes. Then the distance of the vertex of this square which is nearest to the origin is
13
6
The correct Answer is:A
Centre of given circle (3,-4) and Radius =
Vertices of inscribed square will be
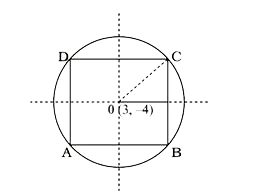
So, vertex nearest to origin will be (-5,4)
Hence required distance =
Topper's Solved these Questions
Similar Questions
A square is inscribed in the circle x2+y2−2x+4y−93=0 with its sides are parallel to coordinate axes then vertices of square are
View SolutionA square is incribed in a circle x2+y2−6x+8y−103=0 such that its sides are parallel to co-ordinate axis then the distance of the nearest vertex to origin, is equal to (A) 13 (B) √127 (C) √41 (D) 1
View SolutionA square is incribed in a circle x2+y2−6x+8y−103=0 such that its sides are parallel to co-ordinate axis then the distance of the nearest vertex to origin, is equal to (A) 13 (B) √127 (C) √41 (D) 1
View SolutionIf an equilateral triangle is inscribed in the circle x2+y2−6x−4y+5=0 then its side is
View SolutionA square is inscribed in the circle x2+y2−2x+4y+3=0 . Its sides are parallel to the coordinate axes. One vertex of the square is (1+√2,−2) (b) (1−√2,−2) (1,−2+√2) (d) none of these
View Solutiona square is inscribed in the circle x2+y2−10x−6y+30=0. One side of the square is parallel to y=x+3, then one vertex of the square is :
View Solutiona square is inscribed in the circle x2+y2−10x−6y+30=0. One side of the square is parallel to y=x+3, then one vertex of the square is :
View SolutionA square is inscribed in the circle x2+y2−2x+4y−93=0 with its sides parallel to the coordinate axes. The coordinates of its vertices are (−6,−9),(−6,5),(8,−9),(8,5) (−6,−9),(−6,−5),(8,−9),(8,5) (−6,−9),(−6,5),(8,9),(8,5) (−6,−9),(−6,5),(8,−9),(8,−5)
View SolutionThe nearest point on the circle x2+y2−6x+4y−12=0 from (-5,4) is
View SolutionA right angled isoceles triangle is inscribed in the circle x2+y2−6x+10y−38=0 then its area is (square units)
View Solution