A thin disc of mass M and radius R has mass per unit area σ(r)=kr2 where r is the distance from its centre. Its moment of inertia about an axis going through its centre of mass and perpendicular to its plane is : a) MR33 b) 2MR23 c) MR26 d) MR22
The correct Answer is:0.67
Disc can be understood as the combination of co-axial rings.
M.I. of element ring of radius r and infinitesimally small thickness dr about the axis is
dI=(dm).r2={(kr2)2πrdr}r2
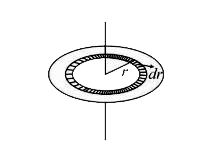
⇒I=2πkR6/6 ...........(1)
Also, mass of ring, M=∫dm=∫Rr=0(kr2)(2πrdr)
Or, M=2πkR44........(2)
From (2) and (2)
I=46MR2=23MR2
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST -14 EXERCISE - PHYSICS (SECTON 2)5videos
JEE MAIN REVISION TEST -14
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST - 7|JEE - 2020EXERCISE - Physics (Section -2) (Numerical Value Type)5videos
JEE MAIN REVISION TEST - 7|JEE - 2020
- BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST -17 (2020)EXERCISE - PHYSICS25videos
JEE MAIN REVISION TEST -17 (2020)
Similar Questions
A semicircular lamina of mass m and radius r and centre C. Its center of mass is at a distance x from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
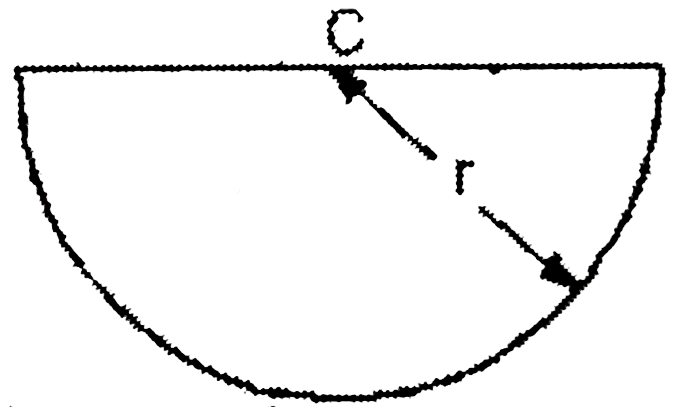 View Solution
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionA disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
View SolutionA disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
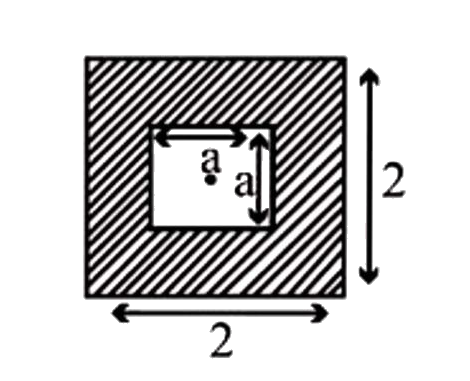 View Solution
View SolutionThe moment of inertia of a uniform cicrular disc about its diameter is 200gcm2. Its moment of inertia about an axis passing through its centre and perpendicular to its circular face is
View SolutionThe moment of inertia of a uniform cicrular disc about its diameter is 200gcm2. Its moment of inertia about an axis passing through its centre and perpendicular to its circular face is
View SolutionA uniform thin bar of mass 6m and length 12L is bend to make a regular hexagon. Its moment of inertia about an axis passing through the centre of mass and perpendicular to the plane of the hexagon is :
View Solution

