A disc of radius R has a concentric hole of radius R /2 and its mass is M. Its moment of inertia about an axis through its centre and perpendicular to its plane, is
12MR2
MR2
38MR2
58MR2
To find the moment of inertia of a disc with a concentric hole, we can follow these steps:
Step 1: Understand the Problem
We have a disc of radius R with a concentric hole of radius R2. The total mass of the disc is M. We need to find the moment of inertia about an axis through its center and perpendicular to its plane.
Step 2: Calculate the Area of the Disc and the Hole
The area of the full disc is:
Adisc=πR2
The area of the hole is:
Ahole=π(R2)2=πR24
Step 3: Calculate the Area of the Annular Region
The area of the annular region (the disc minus the hole) is:
Aannulus=Adisc−Ahole=πR2−πR24=πR2(1−14)=πR2⋅34=3πR24
Step 4: Calculate the Mass Density
The mass density σ of the annular region is given by:
σ=MAannulus=M3πR24=4M3πR2
Step 5: Calculate the Mass of the Hole
The mass of the hole can be calculated using its area and the mass density:
Mhole=σ⋅Ahole=(4M3πR2)⋅(πR24)=4M3⋅14=M3
Step 6: Calculate the Moment of Inertia of the Full Disc
The moment of inertia Idisc of the full disc about its center is:
Idisc=12MR2
Step 7: Calculate the Moment of Inertia of the Hole
The moment of inertia Ihole of the hole (considered as a negative mass) about the same axis is:
Ihole=12Mhole(R2)2=12(M3)(R24)=MR224
Step 8: Calculate the Total Moment of Inertia
The total moment of inertia Iz of the disc with the hole is:
Iz=Idisc−Ihole=12MR2−MR224
To combine these, we need a common denominator:
Iz=12MR224−MR224=11MR224
Final Answer
Thus, the moment of inertia of the disc with a concentric hole about an axis through its center and perpendicular to its plane is:
Iz=11MR224
We have a disc of radius R with a concentric hole of radius R2. The total mass of the disc is M. We need to find the moment of inertia about an axis through its center and perpendicular to its plane.
The area of the full disc is:
Adisc=πR2
The area of the hole is:
Ahole=π(R2)2=πR24
The area of the annular region (the disc minus the hole) is:
Aannulus=Adisc−Ahole=πR2−πR24=πR2(1−14)=πR2⋅34=3πR24
The mass density σ of the annular region is given by:
σ=MAannulus=M3πR24=4M3πR2
The mass of the hole can be calculated using its area and the mass density:
Mhole=σ⋅Ahole=(4M3πR2)⋅(πR24)=4M3⋅14=M3
The moment of inertia Idisc of the full disc about its center is:
Idisc=12MR2
The moment of inertia Ihole of the hole (considered as a negative mass) about the same axis is:
Ihole=12Mhole(R2)2=12(M3)(R24)=MR224
The total moment of inertia Iz of the disc with the hole is:
Iz=Idisc−Ihole=12MR2−MR224
To combine these, we need a common denominator:
Iz=12MR224−MR224=11MR224
Thus, the moment of inertia of the disc with a concentric hole about an axis through its center and perpendicular to its plane is:
Iz=11MR224
Topper's Solved these Questions
Similar Questions
A disc of mass m and radius R has a concentric hole of radius r. Its moment of inertia about an axis through its center and perpendicular to its plane is
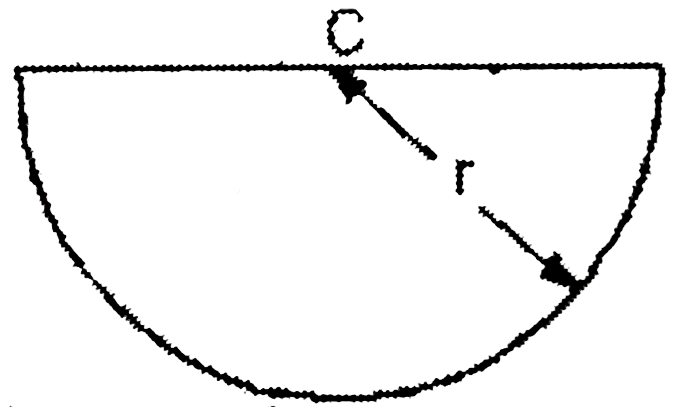
View SolutionA semicircular lamina of mass m and radius r and centre C. Its center of mass is at a distance x from C. Its moment of inertia about an axis through its center of mass and perpendicular to its plane is:
View SolutionA circular disc of radius R and thickness R6 has moment of inertia about an axis passing through its centre and perpendicular to its plane. It is melted and recasted into a solid sphere. The moment of inertia of the sphere about its diameter as axis of rotation is
View SolutionA hole of radius R/2 is removed from a thin circular plate of radius R and mass M. The moment of inertia of the remaining plate about an axis through centre O and perpendicular to the plane of the plate is

View SolutionA thin disc of mass M and radius R has mass per unit area σ(r)=kr2 where r is the distance from its centre. Its moment of inertia about an axis going through its centre of mass and perpendicular to its plane is : a) MR33 b) 2MR23 c) MR26 d) MR22
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionMoment of inertia of a uniform quarter disc of radius R and mass M about an axis through its centre of mass and perpendicular to its plane is :
View SolutionThe diagram shows a uniform disc of mass M & radius 'a', if the moment of inertia of the disc about the axis XY is I, its moment of inertia about an axis through O and perpendicular to the plane of the disc is

View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
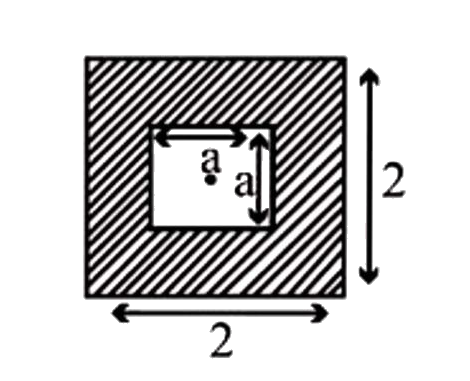
View SolutionA square of a side a is cut from a square of side 2a as shown in the figure. Mass of this square with a hole is M. Then its moment of inertia about an axis passing through its centre of mass and perpendicular to its plane will be
View Solution
