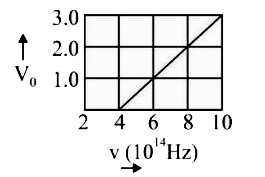
The stopping potential V0 (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be:
(Given : Planck’s constant)
(h)=6.63×10−34Js electron charge e=1.6×10−19C)
1.95 eV
2.12 eV
1.66 eV
1.82
The correct Answer is:C
W=hv0=6.63×10−34×1014×4J
W=6.63×1020J×4=4×6.63×10−201.6×10−19eV=1.66eV
Topper's Solved these Questions
- JEE MAIN REVISION TEST- 16BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST- 16EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST 8 (2020)BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST 8 (2020)EXERCISE - PHYSICS (SECTION 2)
5 Videos
- JEE MAIN REVISION TEST- 24 BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISION TEST- 24 EXERCISE - PHYSICS ( SECTION - 2)
5 Videos
Similar Questions
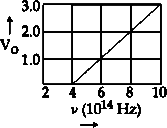
the stopping potential Vo (in volt) as a function of frequency (v) for a soidum emitter, is shown in the figure. The work function of sodium from the data plotted in the figure. Will be:
[ given plank's constant (h)=6.63×10−34Js, electron charge e=1.6×10−19C)
View SolutionThe wavelength of th first spectral line of sodium 5896 Å . The fisrt excitation potential of sodium atomm will be (Planck's constant h=6.63×10−34J−s)
View Solution
Knowledge Check
A student performs an experiment on photoelectric effect using two materials A and B. A plot of stopping potential (V0) vs freqency (v) is as shown in the figure.
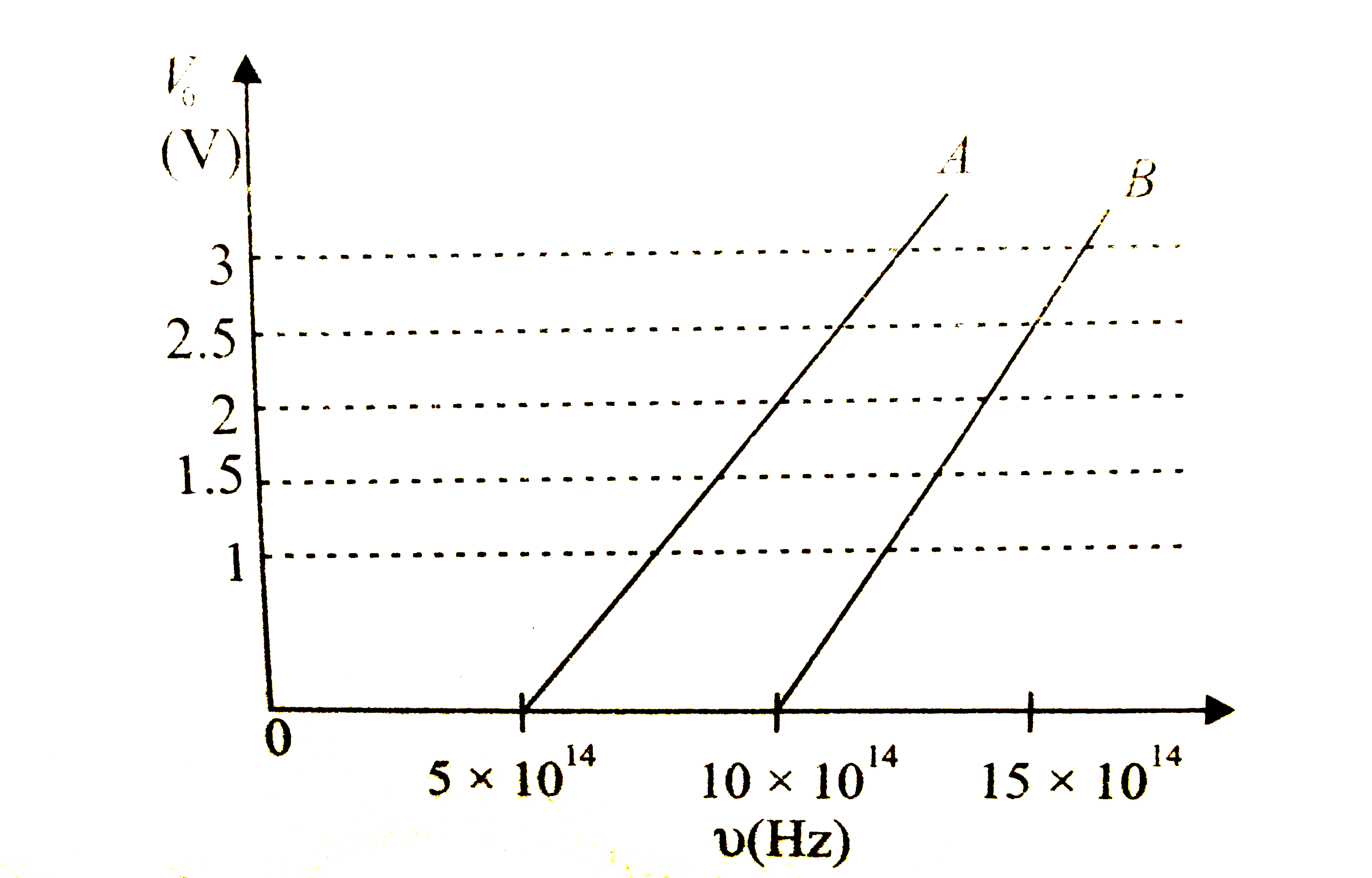
The value of h obtained from the experiment for both A and B respectively is
(Given electric charge of an electron =1.6×10−19C)A3.2×10−34Js,4×10−34JsB6.4×10−34Js,8×10−34JsC1.2×10−34Js,3.2×10−34JsD4.2×10−34Js,5×10−34JsCalculate the energy in joule corresponding to light of wavelength 45 nm : (Planck's constant h=6.63×10−34 Js: speed of light :c=3×108ms−1).
A6.67×1015B6.67×1011C4.42×10−15D4.42×10−18in the question number 63, the frequency of emitted photon due to the given transition is (h=6.64×10−34Js,1eV=1.6×10−19J)
A2.46×1010HzB2.46×1012HzC2.46×1015HzD2.46×1018Hz
What is the number of significant figures in Avogadro's number (6.0×1023) and Planck's constant (6.62×10−34Js).
View SolutionThe electric field of certain radiation is given by the equation E=200{sin(4π×1010)t+sin(4π×1015)t}
falls in a metal surface having work function 2.0 eV. The maximum kinetic energy (in eV) of the photoelectrons is [Plank's constant (h)=6.63×10−34Js and electron charge e=1.6×10−19C]
View SolutionA 2 mW laser operates at a wavelength of 500 nm. The number of photons that will be emitted per second is: [Given Planck’s constant h=6.6×10−34Js, speed of light c=3.0×108m/s]
View SolutionWhen an electron in hydrogen atom is excited, from its 4th to 5th stationary orbit, the change in angular momentum of electron is (Planck's constant: h=6.6×10−34J−s)
View SolutionWork function of sodium is 2.3 eV. Does sodium show photoelectric emission for orange light (λ=6800Å)?
Given h=6.63×10−34Js
View Solution
