The wavelength of th first spectral line of sodium 5896 Å . The fisrt excitation potential of sodium atomm will be (Planck's constant h=6.63×10−34J−s)
4.2V
3.5V
2.1V
None of these
The correct Answer is:C
To find the first excitation potential of the sodium atom based on the given wavelength of its first spectral line, we can follow these steps:
Step 1: Understand the relationship between energy, frequency, and wavelength
The energy (E) of a photon can be expressed in terms of its frequency (ν) using the equation:
E=hν
Where:
- h is Planck's constant.
We can also express frequency in terms of wavelength (λ) using the speed of light (c):
ν=cλ
Thus, we can rewrite the energy equation as:
E=hcλ
Step 2: Substitute the known values
Given:
- Wavelength λ=5896Å=5896×10−10m
- Planck's constant h=6.63×10−34J s
- Speed of light c=3×108m/s
Substituting these values into the energy equation:
E=(6.63×10−34J s)×(3×108m/s)5896×10−10m
Step 3: Calculate the energy
Now, calculate the energy:
E=(6.63×10−34)×(3×108)5896×10−10
Calculating the numerator:
6.63×10−34×3×108=1.989×10−25J m
Now, divide by the wavelength:
E=1.989×10−255896×10−10
Calculating this gives:
E≈3.37×10−19J
Step 4: Convert energy to electron volts
To convert joules to electron volts, we use the conversion factor:
1eV=1.6×10−19J
Thus, converting the energy:
EeV=3.37×10−19J1.6×10−19J/eV≈2.1eV
Step 5: Conclusion
The first excitation potential of the sodium atom is approximately:
2.1eV
The energy (E) of a photon can be expressed in terms of its frequency (ν) using the equation:
E=hν
Where:
- h is Planck's constant.
ν=cλ
Thus, we can rewrite the energy equation as:
E=hcλ
Given:
- Wavelength λ=5896Å=5896×10−10m
- Planck's constant h=6.63×10−34J s
- Speed of light c=3×108m/s
E=(6.63×10−34J s)×(3×108m/s)5896×10−10m
Now, calculate the energy:
E=(6.63×10−34)×(3×108)5896×10−10
6.63×10−34×3×108=1.989×10−25J m
E=1.989×10−255896×10−10
E≈3.37×10−19J
To convert joules to electron volts, we use the conversion factor:
1eV=1.6×10−19J
EeV=3.37×10−19J1.6×10−19J/eV≈2.1eV
The first excitation potential of the sodium atom is approximately:
2.1eV
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - ASSERTION AND REASON10videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - MATCH THE COLUMNS4videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - ATOMSEXERCISE - Check point 12.315videos
ATOMS
- BOOK - DC PANDEY ENGLISHCHAPTER - ALTERNATING CURRENTEXERCISE - JEE MAIN62videos
ALTERNATING CURRENT
- BOOK - DC PANDEY ENGLISHCHAPTER - CAPACITORSEXERCISE - OBJECTIVE_TYPE1videos
CAPACITORS
Similar Questions
The wavelength of line of sodium is 589.6 nm. Express it in Angstrom unit.
View SolutionThe stopping potential V0 (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be:
(Given : Planck’s constant)
(h)=6.63×10−34Js electron charge e=1.6×10−19C)
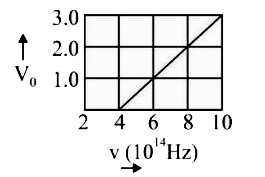 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The de-Broglie wavelength of a tennis ball of mass 60 g moving with a velocity of 10 m/s is approximately (Plank's constant h=6.63×10−34Js)
A10−33mB10−31mC10−16mD10−25m
Hydrogen atom in its ground state is excited by means of monochromatic radiation of wavelength 970.6Å. How many lines are possible in the resulting emission spectrum ? Calculate the longest wavelength amongst them. You may assume that the ionisation energy for hydrogen atom is 13.6 eV. Given Planck's constant =6.6×10−34Js, c=3×10(8)ms−1
View SolutionWhen an electron in hydrogen atom is excited, from its 4th to 5th stationary orbit, the change in angular momentum of electron is (Planck's constant: h=6.6×10−34J−s)
View Solution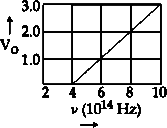
the stopping potential Vo (in volt) as a function of frequency (v) for a soidum emitter, is shown in the figure. The work function of sodium from the data plotted in the figure. Will be:
[ given plank's constant (h)=6.63×10−34Js, electron charge e=1.6×10−19C)View SolutionA 160 watt light source is radiating light of wavelength 6200Å uniformly in all directions. The photon flux at a distance of 1.8m is of the order of (Plank's constant 6.62×10−34J−s)
View SolutionA beam of electrons of energy E scatters from a target having atomic specing of 1Å. The first maximum intensity occurs at θ=60∘. The E (in eV) is ___________
(Planck constant h=6.64×10−34Js,
1eV=1.6×1019J,
electron mass m=9.1×10−31kg)View SolutionIf the deBroglie wavelenght of an electron is equal to 10−3 times the wavelength of a photon of frequency 6×104Hz ,then the speed of electron is equal to (Speed of light =3×108m/s
Planck's constant =6.63×10−34 J s
Mass of electron =9.1×10−31 kgView SolutionThe de - Broglie wavelength of a ball of mass 120 g moving at a speed of 20 m s−1 is (Planck's constant h=6.6×10−34Js)
View Solution

