A semi cylindrical shell with negligible thickness oscillates without slipping on a horizontal surface. The time period of small oscillations is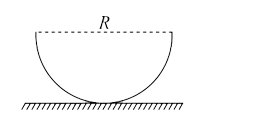 
2π√R(π−2)g
2π√R(π−1)g
2π√R(π+2)g
2π√R(π+1)g
The correct Answer is:A
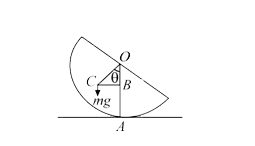
OC=2Rπ
Restoring torque =-mg(BC)
Iα=−mg(2Rπsinθ)
We have I=2mr2(π−2)π
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
The time period of small oscillations of mass m :-
_S01_040_Q01.png)
A2π√m6kB2π√11m6KC2π√6m11KD2π√mK
A solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.
View SolutionA solid sphere (radius=R) rolls without slipping in a cylindrical throuh(radius=5R). Findthe time period of small oscillations.
View SolutionA solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.
View SolutionA solid sphere of mass m is attached to a light spring of force constant k so that it can roll without slipping along a horizontal surface. Calculate the period of oscillation made by sphere.
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.
View SolutionA ring of mass m and radius r rolls without slipping on a fixed hemispherical surface of radius R as shown. The time period of small oscillations of ring is 2π√n(R−r)3g then find the value of n.
View SolutionA small block oscillates back and forth on a smooth concave surface of radius R. Find the time period of small oscillation.
View Solution