A satellite of mass m is launched vertically upwards with an initial speed U from the surface of the Earth. After it reaches height 2 R (R = radius of Earth) it ejects a rocket of mass m5 So, that subsequently the satellite moves in a circular orbit. The kinetic energy of rocket is (M is mass of Earth)
5K2
66K5
33K10
10K
The correct Answer is:C
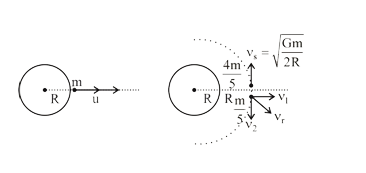
K=12mu2 ∴12mu2−GMmR=12mv2−GMm2R
⇒K−K=12mv2−K2−K2 ⇒mv=m5v1
⇒v1=5valso,4m5VS=m5V2
⇒V2=4VS ∴Krocket=12(m5)(V21+V22)
=m10(25V2+16V2S)=52mv2+85mv2S=52K+4K5=3310K
Topper's Solved these Questions
Similar Questions
A satellite of mass m is launched vertically upwards with initial kinetic energy K from the Earth’s surface. After it reaches height R (R = radius of earth). It ejects a rocket of mass m5 so that subsequently the satellite moves in a circular orbit. The kinetic energy of rocket is [G is gravitational constant, M is the mass of the earth, take GMmR=K]
View SolutionA satellite of mass m is launched vertically upwards with an initial speed √GM® from the surface of the earth. After it reaches height R (R = radius of the earth), it ejects a rocket of mass m10 in a direction opposite to the initial direction of the satellite, so that subsequently the satellite escapes to infinity. The minimum kinetic energy of the rocket at ejection needed is (G is the gravitational constant, M is the mass of the earth):
View SolutionA satellite of mass 'M' is projected radially from surface of earth with speed 'u'. When is reaches a height equal to radius of earth, it ejects a rocket of mass M10and it itself starts orbiting the earth in circular path of radius 2R, find the kinetic energy of rocket.
View SolutionA satellite of mass m0 is revolving around the earth in circular orbit at a height of 3R from surface of the earth the areal velocity of satellite is (where R is radius of earth and M0 is the mass of earth)
View SolutionGravitational potential at a height R from the surface of the earth will be [Take M = mass of the earth, R = radius of the earth]
View SolutionA satellite of mass m is revolving around the Earth at a height R above the surface of the Earth. If g is the gravitational intensity at the Earth’s surface and R is the radius of the Earth, then the kinetic energy of the satellite will be:
View SolutionA satellite of mass m is revolving around the Earth at a height R above the surface of the Earth. If g is the gravitational intensity at the Earth’s surface and R is the radius of the Earth, then the kinetic energy of the satellite will be:
View SolutionA satellite moves around the earth in a circular orbit with speed v. If m is the mass of the satellite, its total energy is
View SolutionIf body of mass mhas to be taken from the surface to the earth to a height h=4R, then the amount of energy required is (R = radius of the earth)
View SolutionIf the earth were to spin faster, acceleration due to gravity at the poles :
View Solution
